1 双塔模型

1.1 模型结构

双塔模型可以看作是矩阵补充模型的升级版。可以对用户 ID、用户离散特征和用户连续特征做处理，处理之后得到很多向量，并把这些向量拼起来。

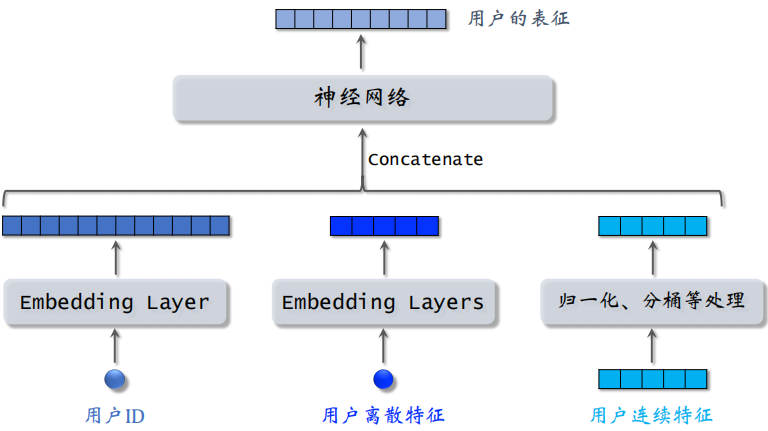
之后输入深度神经网络，神经网络可以是很复杂的结构，神经网络输出一个向量，这个向量就是对用户的表征。

对物品的处理也是类似，如下：

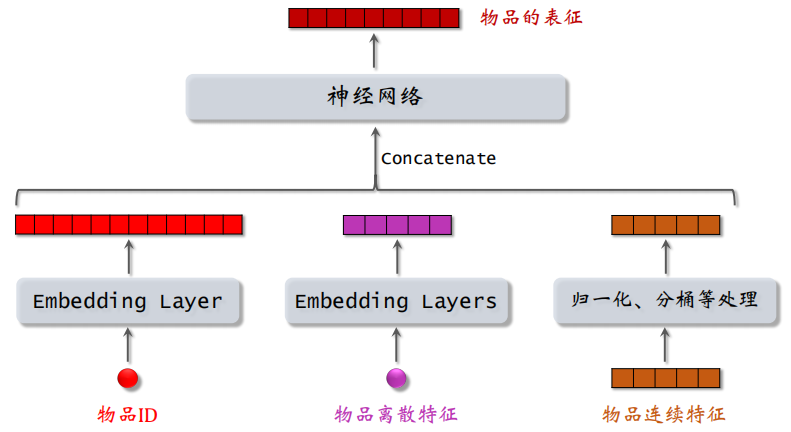
双塔模型的不同之处在于使用了除了 ID 之外的更多的信息来进行处理，如下图所示，可以看到整体结构就像两个塔一样：

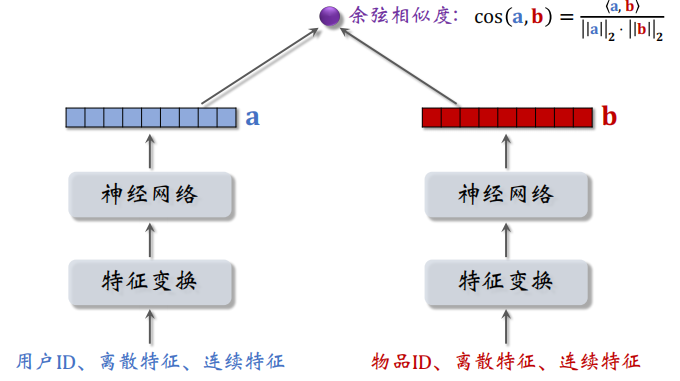
两个塔的输出都是一个向量，之后再计算这两个向量的余弦相似度，余弦相似度的大小介于$[-1, 1]$。

1.2 模型训练

双塔模型的训练可以有以下3种方法：

Pointwise：独⽴看待每个正样本、负样本，做简单的二元分类
Pairwise：每次取一个正样本、一个负样本
Listwise：每次取一个正样本、多个负样本

如何选择正负样本？

正样本：用户点击的物品
负样本：可以有多种定义，比如没有被召回的、召回但是被粗排、精排淘汰的、曝光但是未点击的

1.2.1 Pointwise 训练

把召回看作二元分类任务：

对于正样本，⿎励 $\cos(a,b)$ 接近 $+1$
对于负样本，⿎励 $\cos(a,b)$ 接近 $-1$

一般控制正负样本数量为 $1:2$ 或者 $1:3$

1.2.2 Pairwise 训练

如下图所示，同时取一个正样本和一个负样本，然后经过神经网络得到一个特征向量，正负样本通过的神经网络的参数是相同的（都是物品塔）。

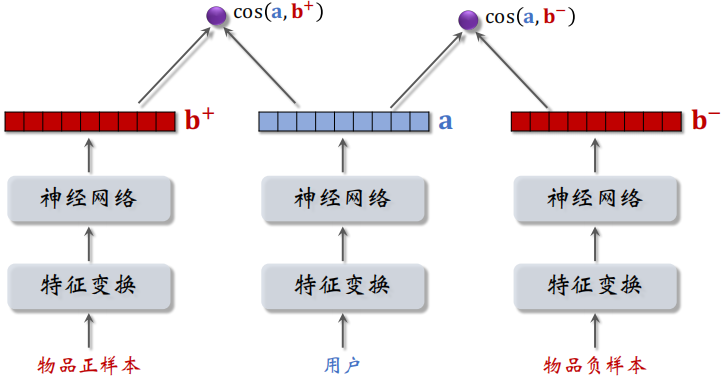
之后分别计算 $\cos(a,b^+)$ 和 $\cos(a,b^-)$ ，模型要鼓励 $\cos(a,b^+)$ 大于 $\cos(a,b^-)$，而且两者之差越大越好。

如果 $\cos(a,b^+)$ 大于 $\cos(a,b^-) + m$，则没有损失。否则，损失等于 $\cos(a, b^-)+m-\cos(a,b^+)$，即鼓励 $\cos(a,b^+)$ 比 $\cos(a,b^-)$ 大 $m$ ，其中 $m$ 是个超参数。

最终的 Triplet hinge loss 如下：

$$
L(\mathbf{a}, \mathbf{b}^{+}, \mathbf{b}^{-})=\max \{0, \cos \left(\mathbf{a}, \mathbf{b}^{-}\right)+m-\cos \left(\mathbf{a}, \mathbf{b}^{+}\right)\}
$$

Triplet logistic loss 如下：

$$
L\left(\mathbf{a}, \mathbf{b}^{+}, \mathbf{b}^{-}\right)=\log \left(1+\exp \left[\sigma \cdot\left(\cos \left(\mathbf{a}, \mathbf{b}^{-}\right)-\cos \left(\mathbf{a}, \mathbf{b}^{+}\right)\right)\right]\right)
$$

训练样本都是三元组，分别为用户、一个正样本和一个负样本。

1.2.3 Listwise 训练

一条数据包括：

一个用户，特征向量记作 $a$
一个正样本，特征向量记作 $b^+$
多个负样本，特征向量记作 ${b}_{1}^{-}, \cdots, {b}_{n}^{-}$

这里鼓励 $\cos \left(\mathrm{a}, \mathrm{b}^{+}\right)$ 尽量大，$\cos \left(\mathrm{a}, {b}_{1}^{-}\right), \cdots, \cos \left(\mathrm{a}, {b}_{n}^{-}\right)$ 尽量小。

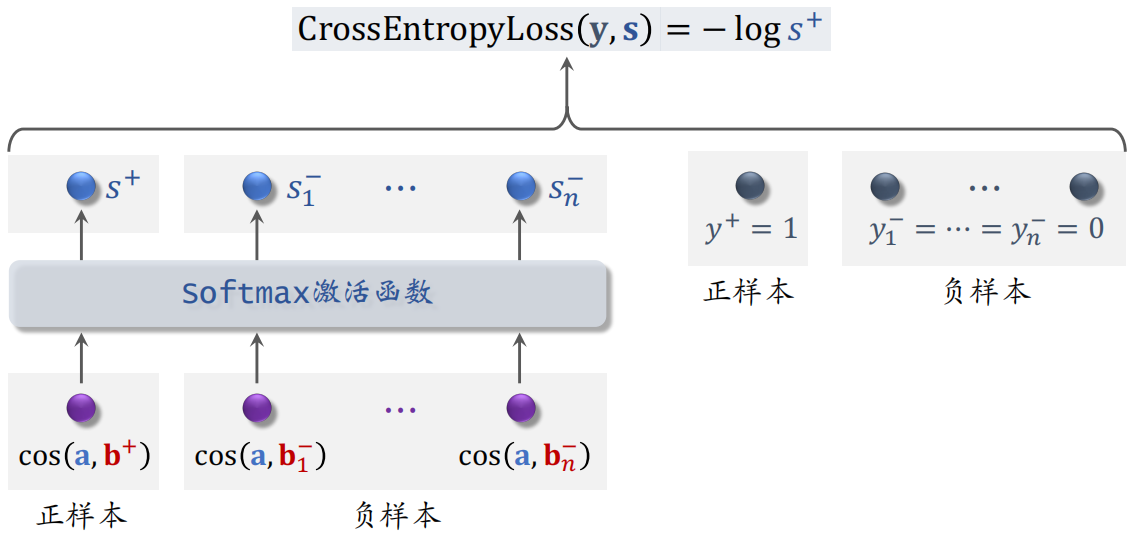
训练的时候把 $n+1$ 个分数输入 Softmax 激活函数，输出 $n+1$ 个分数，这些分数都介于 $0 \sim 1$ 之间。

左边的 $s^+$ 表示正样本的分数，这个分数越大越好，最好能接近1
右边的 $s^-_1 \sim s^-_n$ 表示负样本的分数，希望这些分数越小越好，最好能接近0

用 $y$ 和 $s$ 的交叉熵作为损失函数，训练的时候最小化交叉熵，相当于最大化 $s^+$，也就等价于最大化正样本的余弦相似度，最小化负样本的余弦相似度。

1.3 不适于召回的模型

一看到下面这种结构，就立马反应出是粗排或精排的模型，而不是召回的模型，这种模型没办法应用到召回。

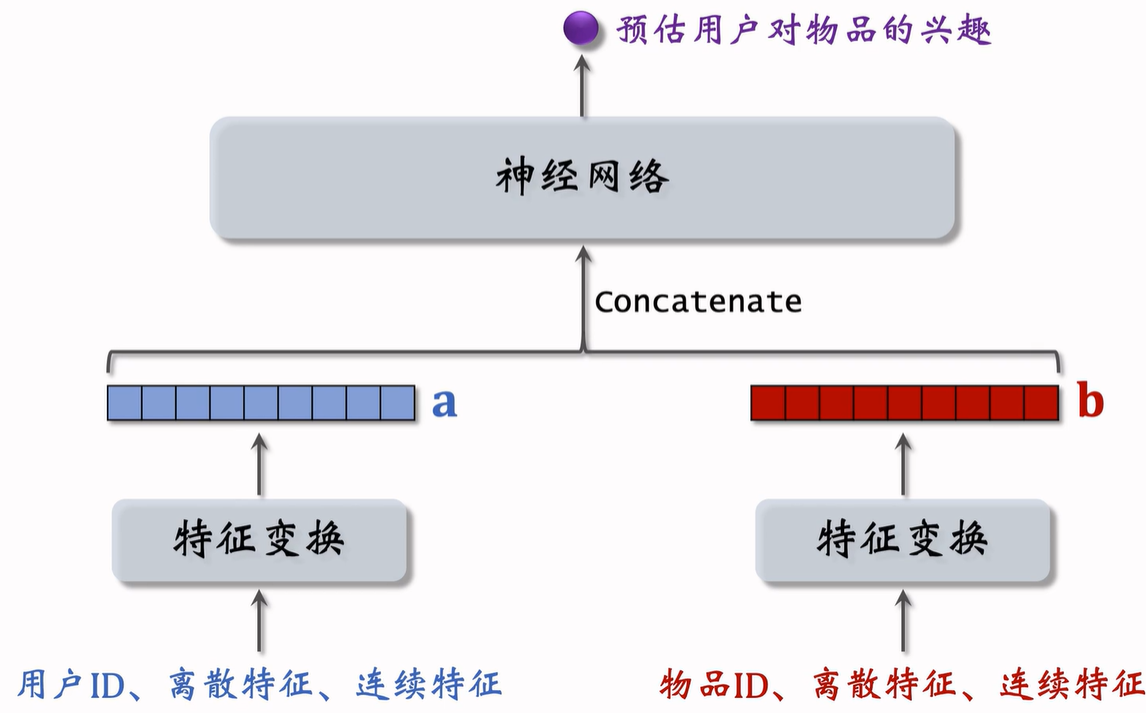
这里在进入神经网络之前直接把两个向量拼接起来，属于前期融合。这种网络架构和双塔结构有很大的区别，双塔模型中两个塔只有在最后输出相似度的时候才融合起来。

这种前期融合的模型不适合于召回，因为需要把用户和所有物品的向量都要拼接起来送入神经网络，时间复杂度较高。

这种模型通常用于排序，从几千个候选物品中选出几百个，计算量不会很大。

2 正负样本

由于双塔模型需要用到正负样本，所以选对正负样本对模型最终的效果至关重要。

2.1 正样本

正样本的选择可以是曝光而且有点击的⽤户—物品⼆元组（⽤户对物品感兴趣）。但是往往正样本都是一些热门物品，导致正样本被点击的次数很多，即少部分物品占据大部分点击。

解决方法：过采样冷门物品，或降采样热门物品。

过采样（up-sampling）：⼀个样本出现多次
降采样（down-sampling）：⼀些样本被抛弃

2.2 负样本

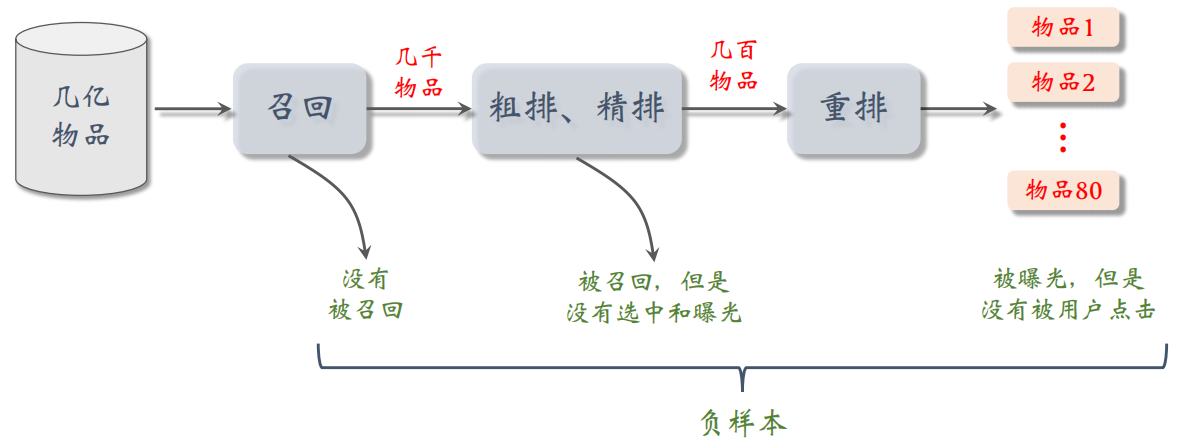
负样本就是用户不感兴趣的物品，也就是推荐系统链路上被淘汰的物品。

2.2.1 简单负样本：全体物品

未被召回的物品，大概率是用户不感兴趣的，所以未被召回的物品 ≈ 全体物品。因此直接从全体物品中做抽样，作为负样本。

问题是怎么做抽样，是均匀抽样还是非均匀抽样。

均匀抽样：对冷门物品不公平

因为正样本大多是热门物品，如果均匀抽样产⽣负样本，负样本⼤多是冷门物品。总拿热门物品做正样本，冷门物品做负样本，对冷门物品会不公平，这样会让热门物品更热，冷门物品更冷。

非均抽采样：目的是打压热门物品

所以应当采用随机非均匀抽样，这样可以打压热门物品抽样的概率与热门程度正相关，热门物品成为负样本的概率大。负样本抽样概率与热门程度（点击次数）正相关。物品的热门程度可以用它的点击次数来衡量，可以按以下方法做抽样，0.75 是个经验值：

$$
抽样概率 \propto(\text { 点击次数 })^{0.75}
$$

上面介绍的简单负样本是从全体物品中抽样的。

2.2.2 简单负样本：Batch内负样本

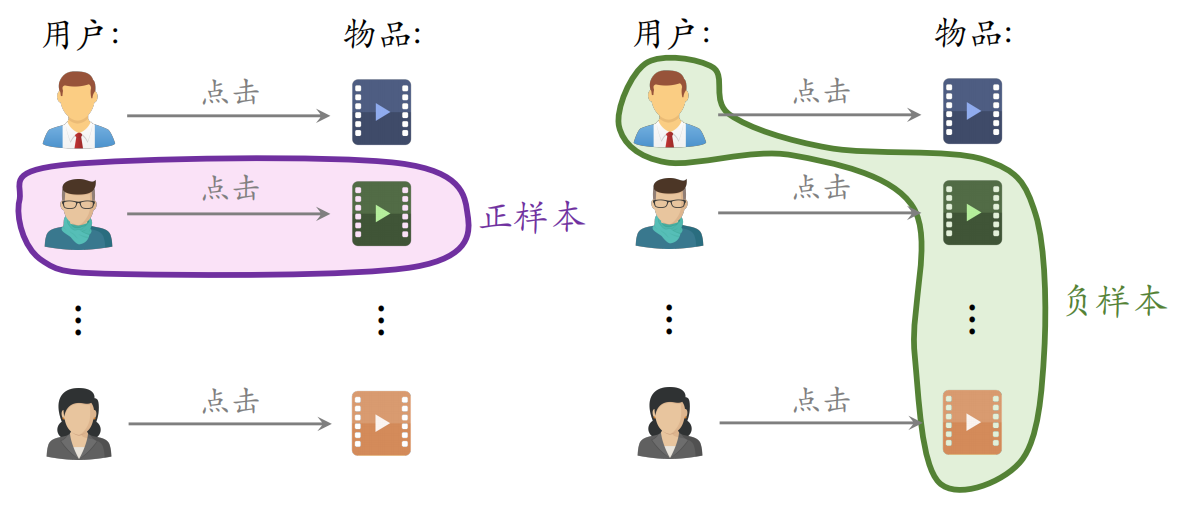
在所曝光的物品中，用户点击了的记为正样本，未点击的记为负样本，⼀个 batch 内有 $n$ 个正样本。⼀个用户和 $n-1$ 个物品组成负样本，则这个 batch 内一共有 $n(n-1)$ 个负样本。但是这些都是是简单负样本，因为第⼀个用户不喜欢第二个物品。

一个物品出现在 batch 内的概率 ∝ 点击次数。但是物品成为负样本的概率本该是 $\propto(\text { 点击次数 })^{0.75}$，但在这里是 ∝ 点击次数。导致热门物品成为负样本的概率过大。

作训练的时候调整为如下公式，线上测试的时候不用调整。

$$
\cos \left(\mathrm{a}, {b}_{i}\right)-\log p_{i}
$$

2.2.3 困难负样本

困难负样本主要有以下两种：

被粗排淘汰的物品（比较困难）
精排分数靠后的物品（非常困难）

困难负样本是指粗排被淘汰的物品，为什么被排序淘汰的物品被称为负样本呢？

因为这些物品被召回，说明和用户的兴趣有点关系，但是粗排被淘汰，说明用户对这些物品的兴趣不够强，所以被分为负样本。对正负样本做二分分类的时候，这些物品容易被分为正样本，容易被分错。

更困难的负样本是通过了粗排，但是在精排中分数排名靠后的物品。

所以在对正负样本做二元分类：

全体物品（简单）分类准确率高
被粗排淘汰的物品（比较困难）容易分错
精排分数靠后的物品（非常困难）更容易分错

在训练的时候混合几种负样本，50%的负样本是全体物品（简单负样本），50%的负样本是没通过排序的物品（困难负样本）。

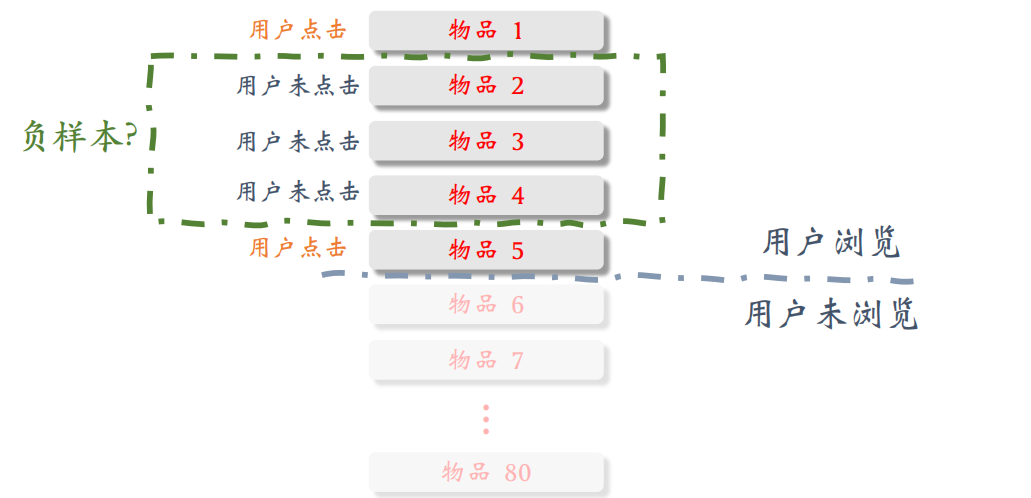
注意，曝光但是没有点击的物品，在训练召回模型不能用这类负样本，训练排序模型会用这类负样本。

2.2.4 选择负样本的原理

召回的目标是快速找到用户可能感兴趣的物品，排序的目标是选择用户最感兴趣的物品。

全体物品（easy）：绝⼤多数是⽤户根本不感兴趣的
被排序淘汰（hard）：⽤户可能感兴趣，但是不够感兴趣
有曝光没点击（没⽤）：⽤户感兴趣，可能碰巧没有点击

3 线上工作过程

主要分为两部分：离线存储和线上召回。

离线存储：把物品向量 $b$ 存⼊向量数据库。

完成训练之后，用物品塔计算每个物品的特征向量 $b$
把几亿个物品向量 $b$，存入向量数据库（⽐如 Milvus、Faiss、HnswLib）
向量数据库建索引，以便加速最近邻查找

线上召回：查找用户最感兴趣的 $k$ 个物品。

给定用户 ID 和画像，线上用神经网络算用户向量 $a$
最近邻查找：把向量 $a$ 作为 query，调⽤向量数据库做最近邻查找，之后返回余弦相似度最大的 $k$ 个物品，作为召回结果

3.1 离线存储

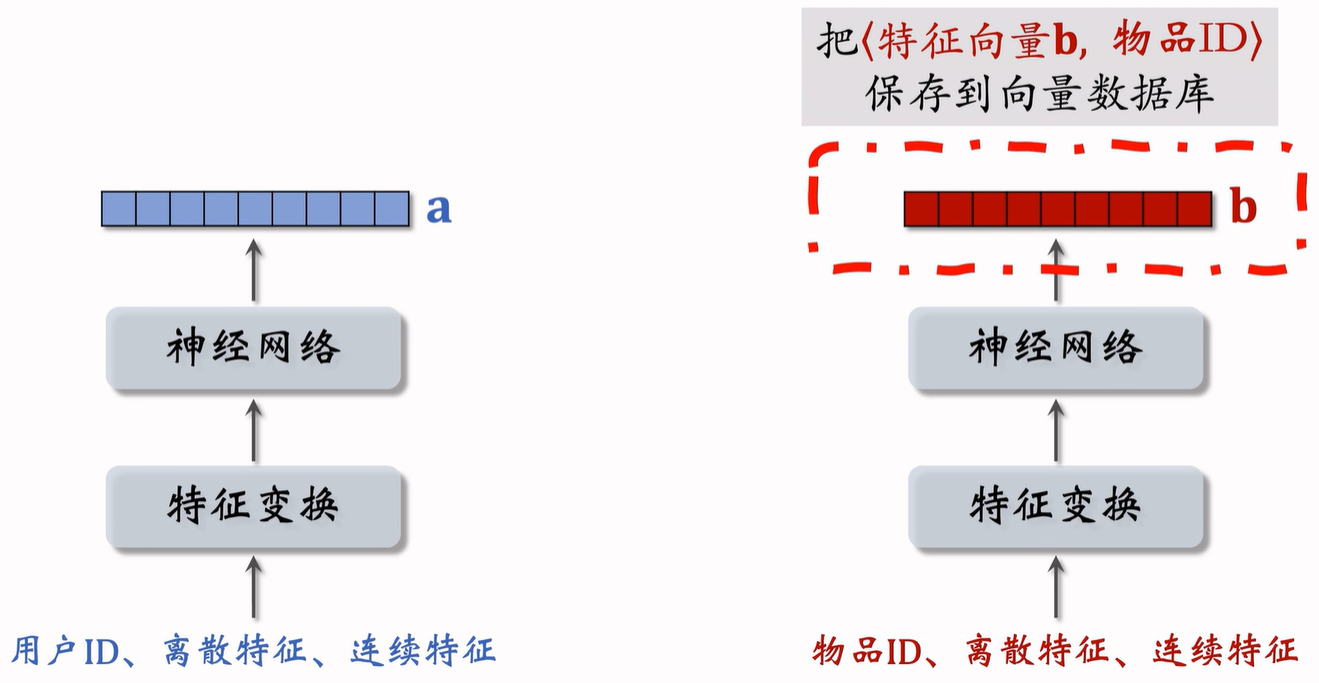
训练得到两个塔之后，就可以做线上召回，把物品ID送入NN之后，得到特征 $b$，并把 $\langle 特征向量b, 物品ID \rangle$ 保存到向量数据库中。

3.2 线上召回

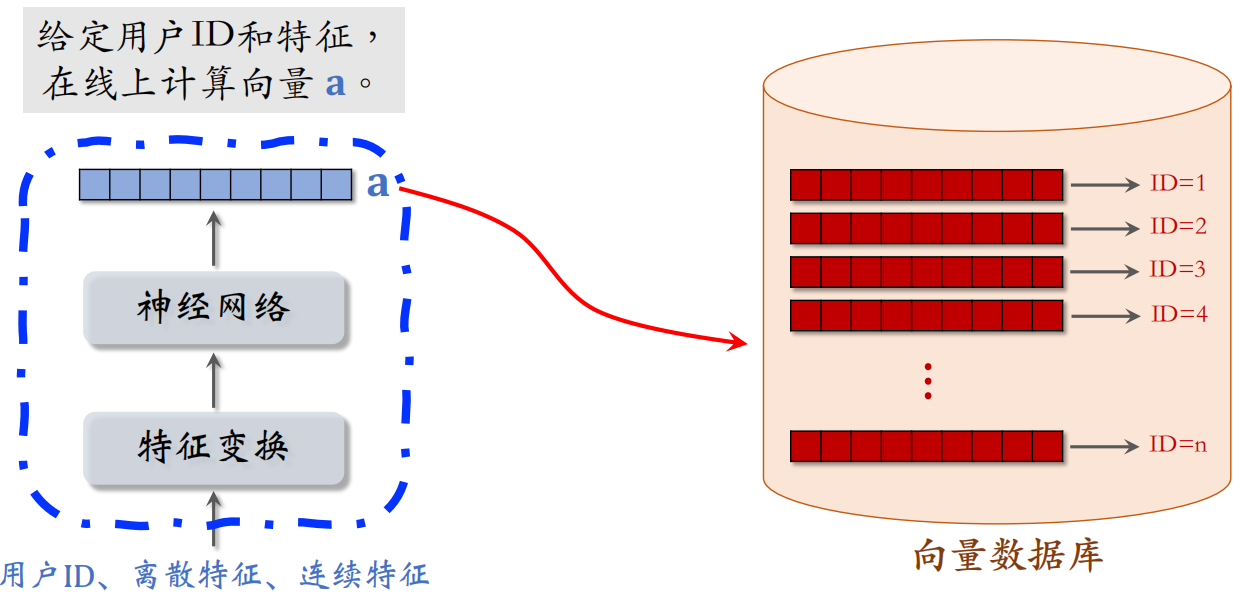
对于用户塔来说，不用事先计算和存储用户向量，而是等用户发起推荐请求的时候，调用神经网络在线上实时计算一个特征向量 $a$，然后把向量 $a$ 作为 $query$ 去数据库中做检索，查找最近邻。

3.3 模型更新

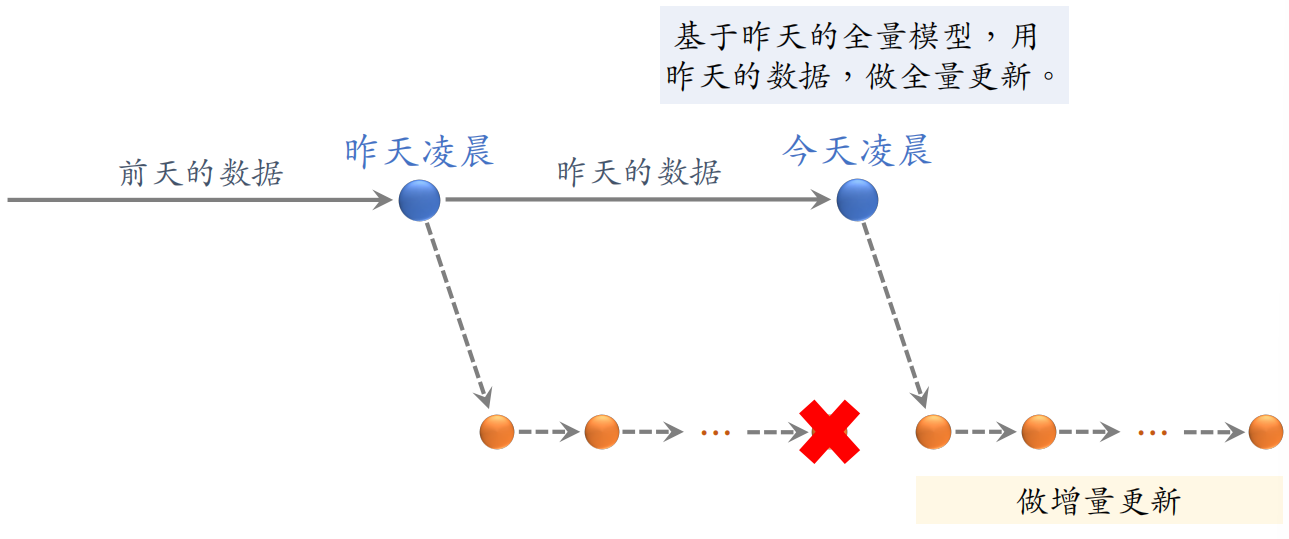
全量更新：今天凌晨，用昨天全天的数据训练模型。是在昨天模型参数的基础上做训练，而不是随机初始化。

用昨天的数据训练 1 epoch，即每天数据只用⼀遍。之后发布新的用户塔神经网络和物品向量，供线上召回使用。全量更新对数据流、系统的要求比较低。

增量更新：做 online learning 更新模型参数。

由于用户兴趣会随时发⽣变化，所以实时收集线上数据做流式处理，生成 TFRecord 文件。即对模型做 online learning，增量更新 ID Embedding 参数（不更新神经网络其他部分的参数）。之后发布 ID Embedding，供⽤户塔在线上计算用户向量。

问题：能否只做增量更新，不做全量更新？

由于小时级数据有偏，并且分钟级数据偏差更大，所以不能只做增量更新。

全量更新：random shuffle ⼀天的数据，做 1 epoch 训练
增量更新：按照数据从早到晚的顺序，做 1 epoch 训练

随机打乱优于按顺序排列数据，所以全量训练优于增量训练。

4 自监督学习改进双塔模型

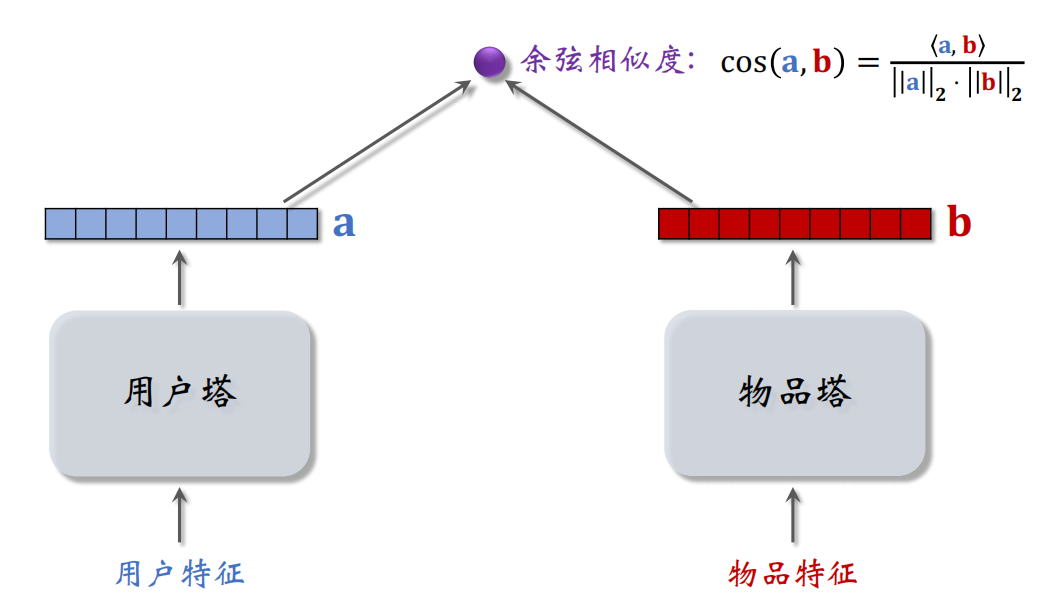
双塔模型整体分为两个塔：用户塔和物品塔。之后将两个塔输出的向量做余弦相似度的计算，得到用户 $a$ 对物品 $b$ 的感兴趣的分数。

双塔模型的问题：

推荐系统的头部效应严重：少部分物品占据大部分点击，大部分物品的点击次数不高。
高点击物品的表征学得好，长尾物品的表征学得不好。

解决方法：可以使用自监督学习，即做 data augmentation，更好地学习长尾物品的向量表征。

4.1 使用自监督学习训练物品塔

现在有两个物品 $i$ 和 $j$，对它们做不同的特征变换分别得到 $i’$、$i’’$ 和 $j’$、$j’’$。把这些特征输入物品塔，下面四个物品塔使用相同的参数。由于使用的特征变换不同，所以通过相同的物品塔得到的 $b^{\prime}_i$ 和 $b^{\prime }_i$不相同，但是两个向量是对同一个物品的表征，所以应该有比较高的相似度。

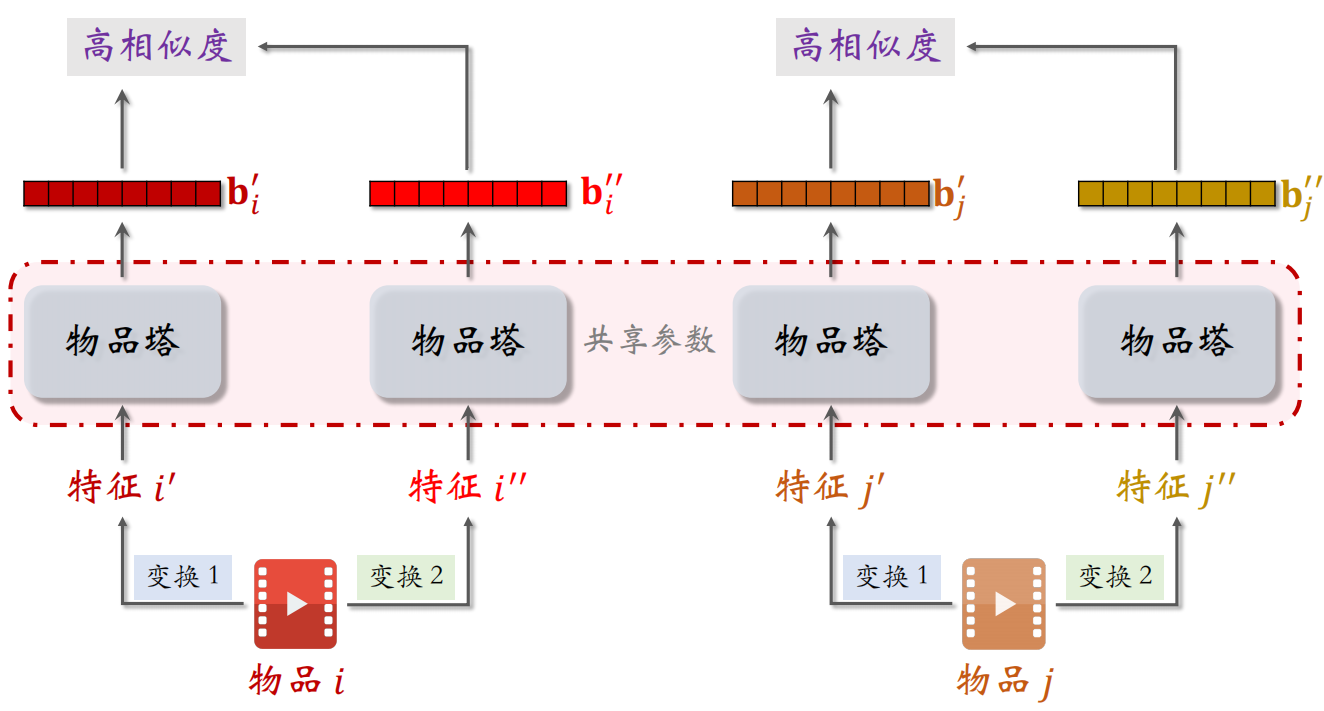
但是不同物品的表征应该距离比较远，不相似。

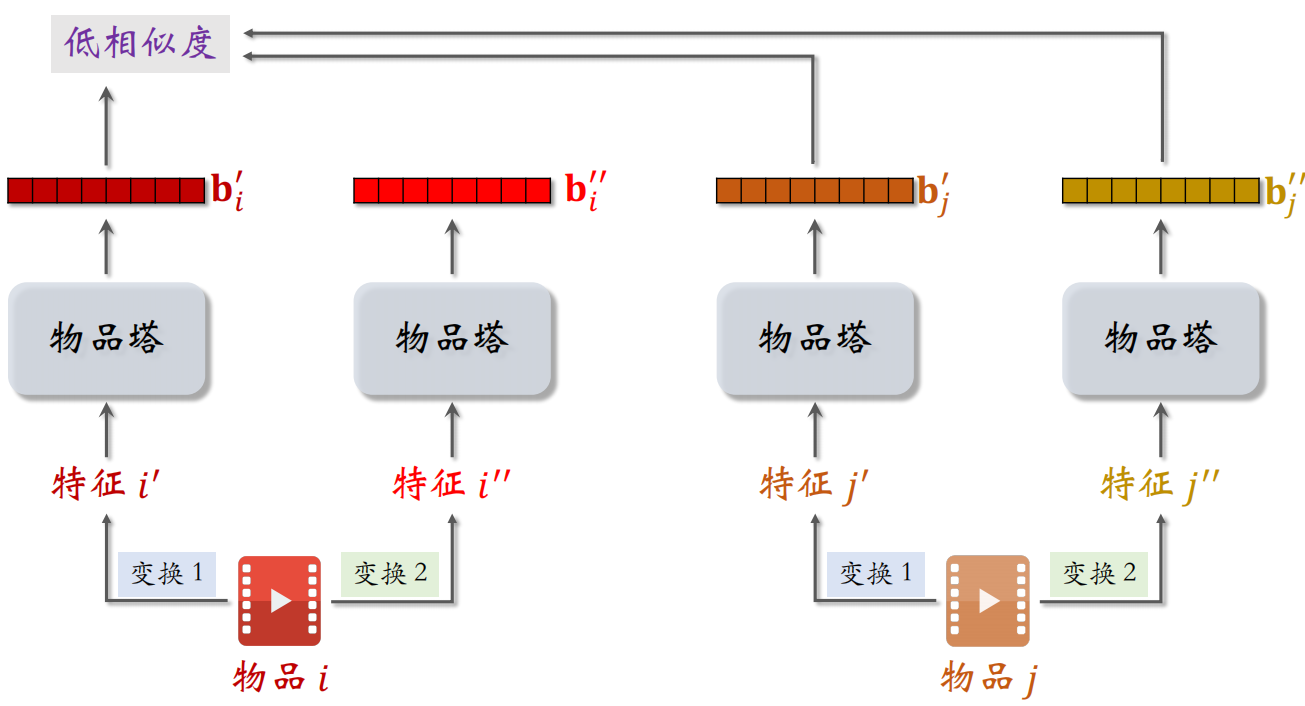
物品 $i$ 的两个向量表征 $b^{\prime}_i$ 和 $b^{\prime \prime}_i$ 有较高的相似度，物品 $i$ 和 $j$ 的两个向量表征 $b^{\prime}_i$ 和 $b^{\prime \prime}_j$ 有较低的相似度，所以鼓励 $\cos \left({b}_{i}^{\prime}, {b}_{i}^{\prime \prime}\right)$ 尽量大，$\cos \left({b}_{i}^{\prime}, {b}_{j}^{\prime \prime}\right)$ 尽量小。

4.2 特征变换方式

4.2.1 Random Mask

随机选⼀些离散特征（⽐如类⽬），把它们遮住。例如：某物品的类⽬特征是 $\mathcal{U} = {数码,摄影}$，Mask 后的类⽬特征是 $\mathcal{U}^{\prime}={ default }$。

相当于 Mask 之后该物品的类目特征就没有了。

4.2.2 Dropout

⼀个物品可以有多个类⽬，那么类⽬是⼀个多值离散特征。Dropout 是指随机丢弃特征中 50% 的值，只对多值离散特征生效。

例如：某物品的类⽬特征是 $\mathcal{U} = {美妆,摄影}$，Mask 后的类⽬特征是 $\mathcal{U}^{\prime}={ 美妆}$。

注意：Random Mask 是把整个类目信息全部丢掉，但是 Dropout 是丢失一部分信息

4.2.3 互补特征（complementary）

假设物品⼀共有 4 种特征：ID，类⽬，关键词，城市，将其随机分为两组：

$$
{ ID，关键词 } 和 { 类目，城市 }
$$

之后分别将其中某一组给 mask 掉，送入物品塔，得到不同的物品表征，则希望输出的两个向量相似。

4.2.4 Mask 一组关联的特征

把一组相关的特征中只保留一个特征，例如：

受众性别：$\mathcal{U}={ 男, 女, 中性 }$
类目：$\mathcal{V}={ 美妆，数码，足球，摄影，科技， \cdots}$

则 $u = 女$ 和 $v = 美妆$ 同时出现的概率 $p(u, v)$ 大，而 $u = 女$ 和 $v = 数码$ 同时出现的概率 $p(u, v)$ 小。

离线计算特征两两之间的关联，用互信息（mutual information）衡量：

$$
\operatorname{MI}(\mathcal{U}, \mathcal{V})=\sum_{u \in \mathcal{u}} \sum_{v \in \mathcal{v}} p(u, v) \cdot \log \frac{p(u, v)}{p(u) \cdot p(v)}
$$

具体工作过程如下：设⼀共有 $k$ 种特征。离线计算特征两两之间 MI，得到 $k \times k$ 的矩阵。随机选一个特征作为种子，找到种子最相关的 $k/2$ 种特征，Mask 种子及其相关的 $k / 2$ 种特征，保留其余 $k/2$ 种特征。

优点：比 random mask、dropout、互补特征等方法效果更好。
缺点：方法复杂，实现的难度⼤，不容易维护。

4.3 模型训练

首先从从全体物品中均匀抽样，得到 $m$ 个物品，作为⼀个batch。双塔模型是根据用户点击量进行抽样的，而这里是进行随机抽样，热门和冷门物品被抽到的概率相同。

之后做两类特征变换，物品塔输出两组向量：

$$
\mathbf{b}_{1}^{\prime}, \mathbf{b}_{2}^{\prime}, \cdots, \mathbf{b}_{m}^{\prime} \quad 和 \quad \mathbf{b}_{1}^{\prime \prime}, \mathbf{b}_{2}^{\prime \prime}, \cdots, \mathbf{b}_{m}^{\prime \prime}
$$

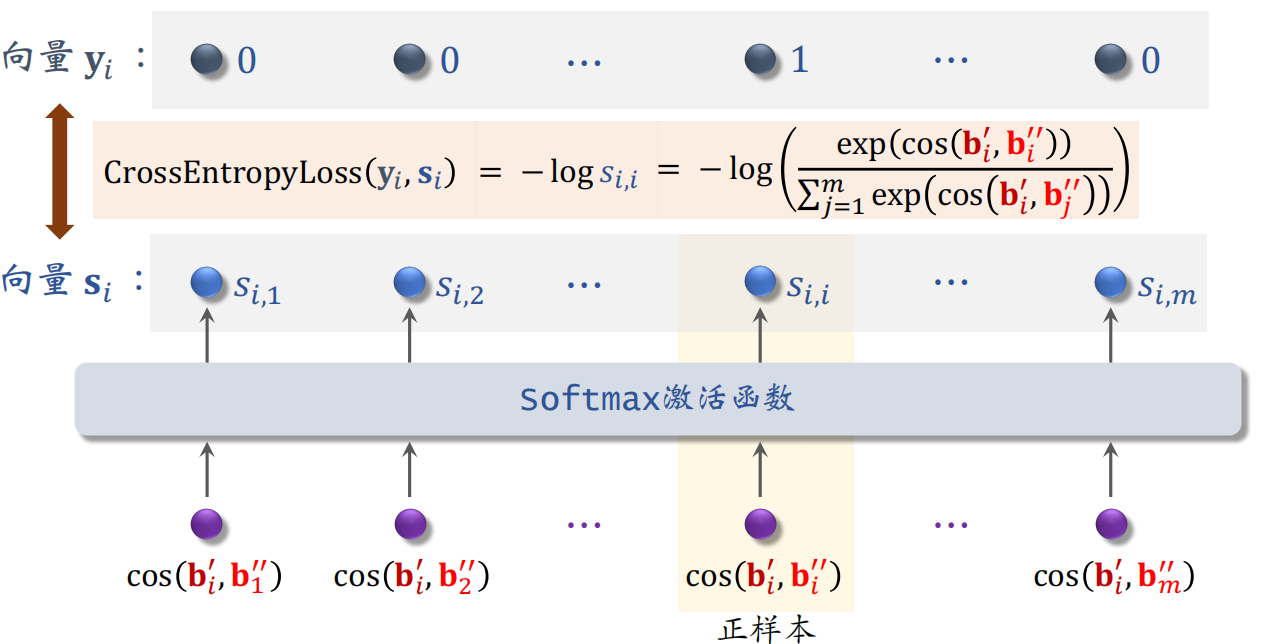
其中第 $i$ 个物品自监督学习的损失函数为：

$$
L_{\text {self }}[i]=-\log \left(\frac{\exp \left(\cos \left(\mathbf{b}_{i}^{\prime}, \mathbf{b}_{i}^{\prime \prime}\right)\right)}{\sum_{j=1}^{m} \exp \left(\cos \left(\mathbf{b}_{i}^{\prime}, \mathbf{b}_{j}^{\prime \prime}\right)\right)}\right)
$$

具体推导如下图，只有第 $i$ 个物品的 $b^{\prime}_i$ 和 $b^{\prime \prime}_i$ 是相似的，而 $b^{\prime}_i$ 和其他剩下的 $m-1$ 个物品是不相似的。