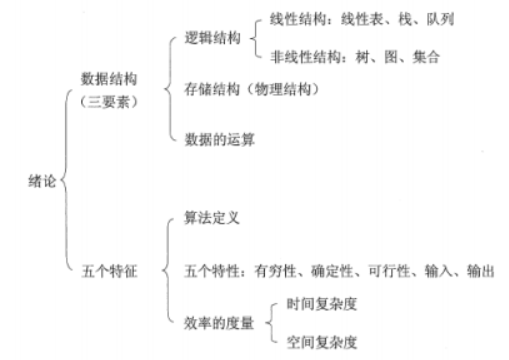
数据结构面经1:绪论
1 时间复杂度
一个语句的频度是指该语句在算法中被重复执行的次数。算法中所有语句的频度之和记为 $T(n)$,它是该算法问题规模 $n$ 的函数。
时间复杂度主要分析 $T(n)$ 的数量级。算法中基本运算(最深层循环内的语句)的频度与 $T(n)$ 同数量级,因此通常采用算法中基本运算的频度$f(n)$来分析算法的时间复杂度。因此,算法的时间复杂度记为
$$
T(n) = O(f(n))
$$
$O$ 的含义是 $T(n)$ 的数量级,其严格的数学定义是:若 $T(n)$ 和 $f(n)$ 是定义在正整数集合上的两个函数,则存在正常数 $C$ 和 $n_0$,使得当 $n \geq n_0$ 时,都满足 $0 \leq T(n) \leq Cf(n)$。
算法的时间复杂度不仅依赖于问题的规模 $n$,也取决于待输入数据的性质(如输入数据元素的初始状态)。
2 空间复杂度
算法的空间复杂度 $S(n)$ 定义为该算法所耗费的存储空间,它是问题规模 $n$ 的函数。记为
$$
S(n)=O(g(n))
$$
一个程序在执行时除需要存储空间来存放本身所用的指令、常数、变量和输入数据外,还需要一些对数据进行操作的工作单元和存储一些为实现计算所需信息的辅助空间。
若输入数据所占空间只取决于问题本身,和算法无关,则只需分析除输入和程序之外的额外空间。
算法原地工作是指算法所需的辅助空间为常量,即 $O(1)$。
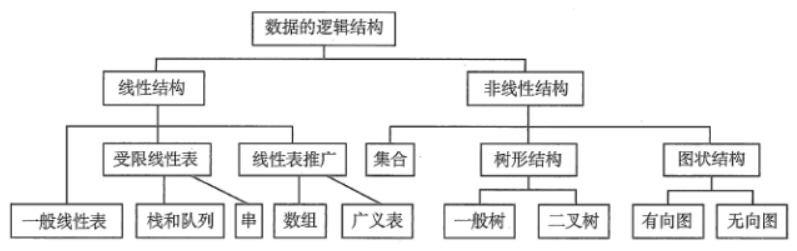
3 数的逻辑结构
数的逻辑结构指的是数据元素之间逻辑关系,与数的存储结构无关,是独立于计算机的,以下是分类图。
4 数的存储结构
存储结构是指数据结构在计算机中的表示,也称物理结构,主要有以下4种:
顺序存储:把逻辑上相邻的元素存储在物理位置上也相邻的存储单元中,元素之间的关系由存储单元的邻接关系来体现。
优点是可以实现随机存取,每个元素占用最少的存储空间;
缺点是只能使用相邻的一整块存储单元,因此可能产生较多的外部碎片。
链式存储:不要求逻辑上相邻的元素在物理位置上也相邻,借助指示元素存储地址的指针来表示元素之间的逻辑关系。
优点是不会出现碎片现象,能充分利用所有存储单元;
缺点是每个元素因存储指针而占用额外的存储空间,且只能实现顺序存取。
索引存储:在存储元素信息的同时,还建立附加的索引表。索引表中的每项称为索引项,索引项的一般形式是(关键字,地址)。
优点是检索速度快;
缺点是附加的索引表额外占用存储空间。另外,增加和删除数据时也要修改索引表,因而会花费较多的时间。
散列存储:根据元素的关键字直接计算出该元素的存储地址,又称哈希(Hash)存储。
优点是检索、增加和删除结点的操作都很快;
缺点是若散列函数不好,则可能出现元素存储单元的冲突,而解决冲突会增加时间和空间开销。
5 用循环比递归的效率高吗?
循环和递归两者是可以互换的,不能决定性的说循环的效率比递归高。
递归的优点是:代码简洁清晰,容易检查正确性;缺点是:当递归调用的次数较多时,要增加额外的堆栈处理,有可能产生堆栈溢出的情况,对执行效率有一定的影响。
循环的优点是:结构简单,速度快;缺点是:它并不能解决全部问题,有的问题适合于用递归来解决不适合用循环。
6 贪心算法和动态规划以及分治法的区别?
贪心算法顾名思义就是做出在当前看来是最好的结果,它不从整体上加以考虑,也就是局部最优解。
- 贪心算法从上往下,从顶部一步一步最优,得到最后的结果,它不能保证全局最优解,与贪心策略的选择有关。
动态规划是把问题分解成子问题,这些子问题可能有重复,可以记录下前面子问题的结果防止重复计算。动态规划解决子问题,前一个子问题的解对后一个子问题产生一定的影响。在求解子问题的过程中保留哪些有可能得到最优的局部解,丢弃其他局部解,直到解决最后一个问题时也就是初始问题的解。
- 动态规划是从下到上,一步一步找到全局最优解。(各子问题重叠)
分治法(divide-and-conquer):将原问题划分成n个规模较小而结构与原问题相似的子问题;递归地解决这些子问题,然后再合并其结果,就得到原问题的解。(各子问题独立)
分治模式在每一层递归上都有三个步骤:
- 分解(Divide):将原问题分解成一系列子问题
- 解决(Conquer):递归地解各个子问题。若子问题足够小,则直接求解
- 合并(Combine):将子问题的结果合并成原问题的解,例如归并排序










