线性代数第4章：向量组的线性相关性

1 向量组及其线性组合

1.1 向量

【定义1】n个有次序的数$a_{1}, a_{2}, \cdots, a_{n}$所组成的数组称为n维向量，这n个数称为该向量的n个分量，第i个数$a_i$称为第i个分量。

1.1.1 向量的表示法

n维向量写成一行，称为行向量，也称为行矩阵，常用$a^{T}, {b}^{T}, \alpha^{T}, \beta^{T}$等表示，如$a^{T}=\left(a_{1}, a_{2}, \cdots, a_{n}\right)$。

n维向量写成一列，称为列向量，也称为列矩阵，常用$a, {b}, \alpha, \beta$等表示。

说明：

1. 行向量和列向量总看成两个不同的向量。
2. 行向量和列向量都按矩阵的运算法则进行运算。
3. 在没有明确说明时，向量均理解为列向量。

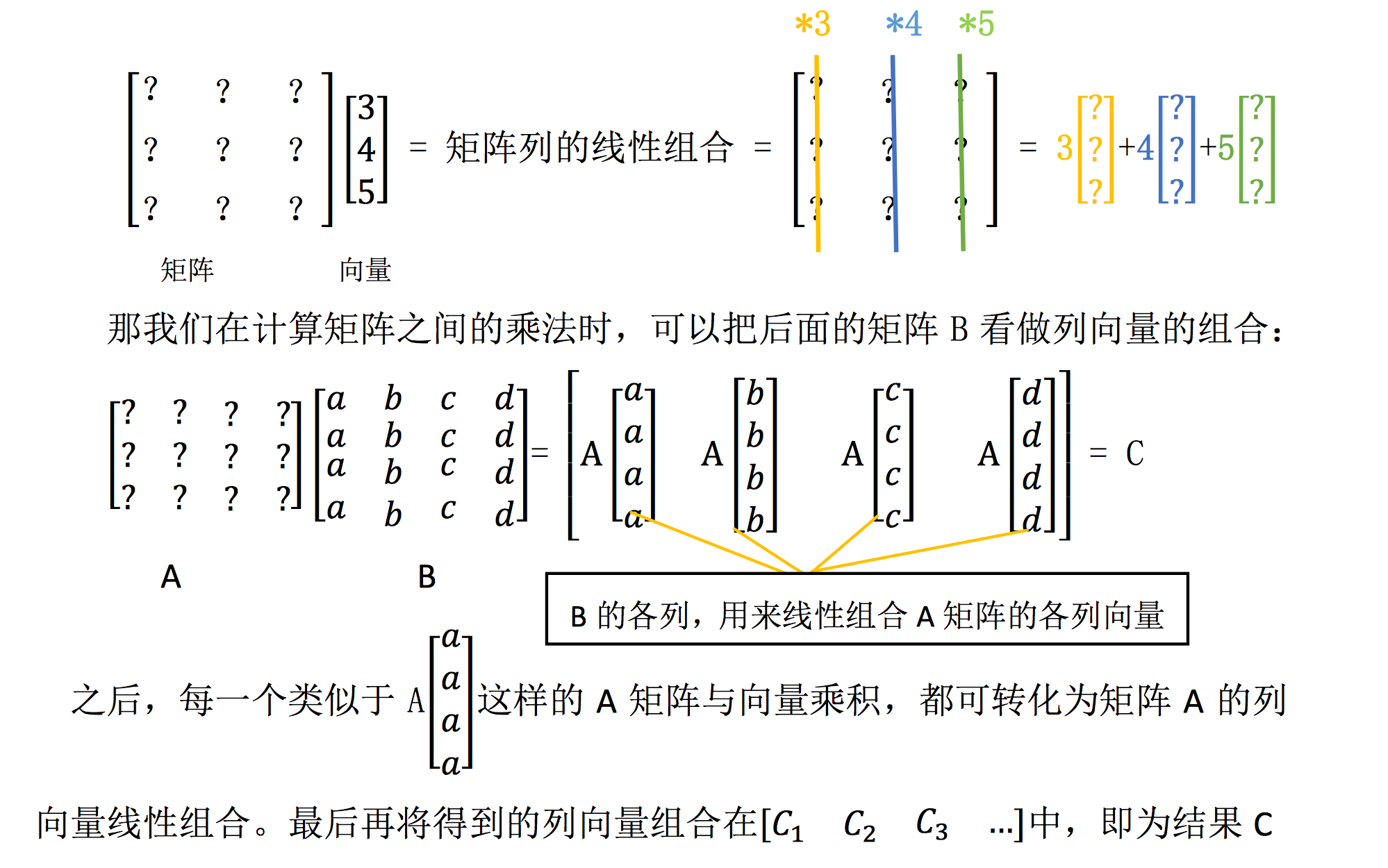
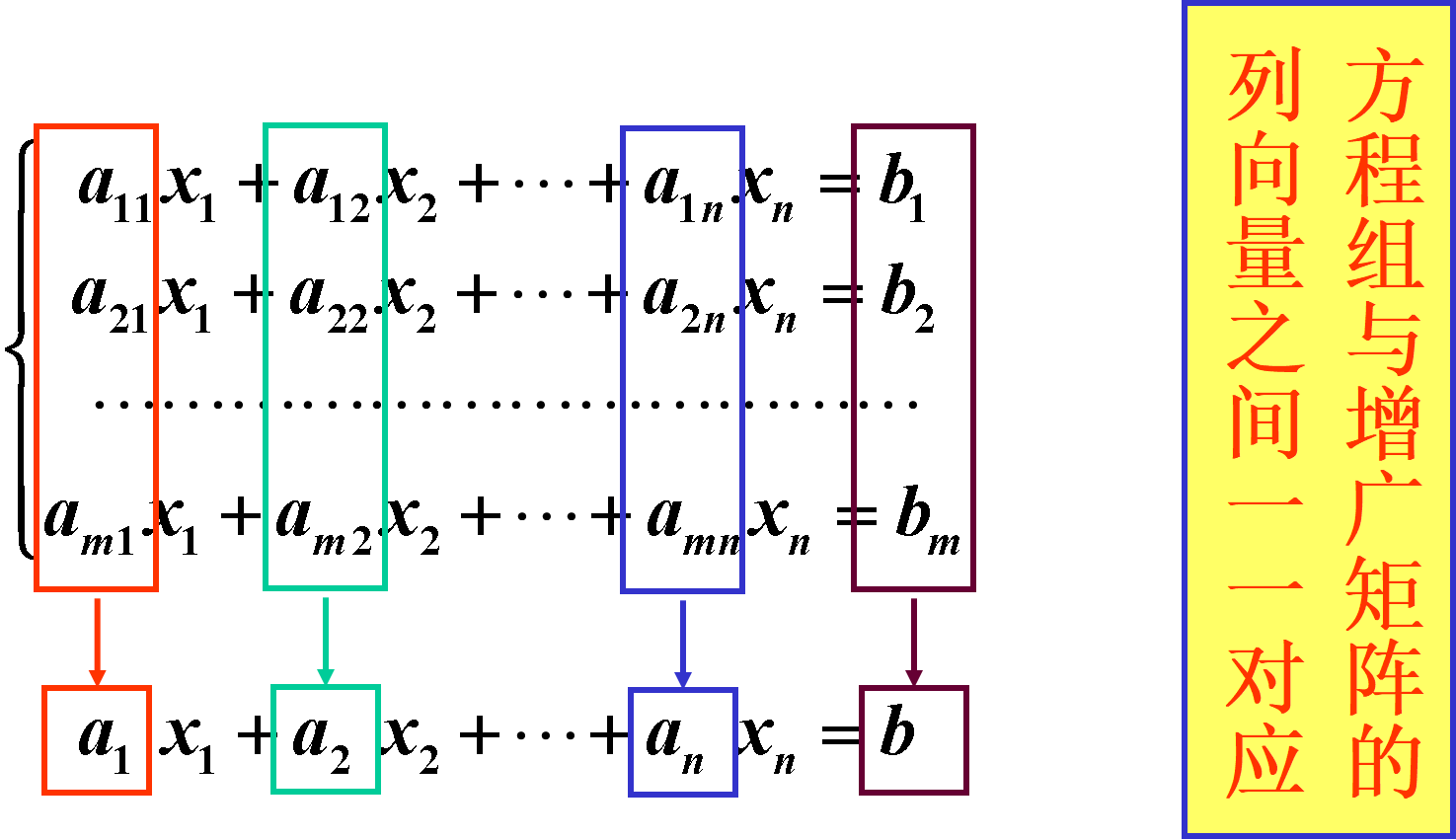
1.2 向量组与矩阵的关系

由若干个同维数的列向量（或同维数的行向量）组成的集合，称为一个向量组。

反之，由有限个向量组成的向量组可以构成一个矩阵。

1.3 线性组合及线性表示

【定义2】给定向量组$A: a_{1}, a_{2}, \cdots, a_{m}$，对于任何一组实数$k_{1}, k_{2}, \cdots, k_{m}$，表达式$k_{1} a_{1}+k_{2} a_{2}+\cdots+k_{m} a_{m}$称为向量组A的一个线性组合，$k_{1}, k_{2}, \cdots, k_{m}$称为这个线性组合的系数。

给定向量组$A: a_{1}, a_{2}, \cdots, a_{m}$和向量b，如果存在一组实数$\lambda_{1}, \lambda_{2}, \cdots, \lambda_{m}$，使得

$b=\lambda_{1} a_{1}+\lambda_{2} a_{2}+\cdots+\lambda_{m} a_{m}$

则向量b是向量A的线性组合，此时称向量b能由向量A线性表示。

【定理1】向量b能由向量组$A: a_{1}, a_{2}, \cdots, a_{m}$线性表示的充要条件是：

$R(A)=R(A,b)$

相当于线性方程组有解。

【定义3】设有两个向量组$A: a_{1}, a_{2}, \cdots, a_{m}$及$B: b_{1}, b_{2}, \cdots, b_{l}$，若向量组B中的每个向量都能由向量组A线性表示，则称向量组B能由向量组A线性表示。若向量组A与向量组B能相互表示，则称两个向量组等价。

可以将向量组的线性组合、线性表示及等价的概念移用到线性方程组。

• 对方程组A的各个方程作线性运算，所得到的方程称为方程组A的一个线性组合。
• 若方程组B的每个方程都是方程组A的线性组合，就称方程组b能由方程组A线性表示，此时方程组A的解一定是方程组B的解。

若方程组A与方程组B能互相表示，就称这两个方程组可互推，互推的方程组一定同解。

【定理3】向量$B: b_{1}, b_{2}, \cdots, b_{l}$能由向量组$A: a_{1}, a_{2}, \cdots, a_{m}$线性表示的充要条件是：

$R(A)=R(A,B)$

【推论】向量组$A: a_{1}, a_{2}, \cdots, a_{m}$与向量组$B: b_{1}, b_{2}, \cdots, b_{l}$等价的充要条件是：

$R(A)=R(B)=R(A,B)$

【定理4】向量$B: b_{1}, b_{2}, \cdots, b_{l}$能由向量组$A: a_{1}, a_{2}, \cdots, a_{m}$线性表示，则：

$R\left(b_{1}, b_{2}, \cdots, b_{l}\right) \leq R\left(a_{1}, a_{2}, \cdots, a_{m}\right)$

---

2 向量组的线性相关性

2.1 线性相关的概念

【定义1】给定向量组$A: a_{1}, a_{2}, \cdots, a_{m}$，若存在不全为0的数$k_{1}, k_{2}, \cdots, k_{m}$，使

$k_{1} a_{1}+k_{2} a_{2}+\cdots+k_{m} a_{m}=0$

则称向量组A是线性相关的，否则称它线性无关。

注意：

1. 向量组$A: a_{1}, a_{2}, \cdots, a_{m}$线性无关，则$k_{1}, k_{2}, \cdots, k_{m}$全为0
2. 对任一向量组，不是线性相关的就是线性无关的
3. 向量组只含有一个向量a时，若$a=0$称向量组是线性相关的，饭之为线性无关
4. 对于含有两个向量的向量组，它是线性相关的充分必要条件是两向量的分量对应成比例。几何意义是两向量共线。三个向量线性相关的几何意义是三向量共面。
5. 包含零向量的向量组是线性相关的。

2.2 线性相关性的判定

【定理1】向量组$a_{1}, a_{2}, \cdots, a_{m}(m \geq 2)$线性相关的充要条件是$a_{1}, a_{2}, \cdots, a_{m}$中至少有一个向量可由其余m-1个向量线性表示。

向量组的线性相关与线性无关的概念可以移用到线性方程组中。

当方程组中某个方程是其余方程的线性组合时，这个方程就是多余的，这时称方程组（各个方程）是线性相关的；

当方程组中没有多余的方程时，就称方程组（各个方程）线性无关（或线性独立）。

向量组A线性相关$\longleftrightarrow$齐次线性方程组$Ax=0$有非0解

【定理2】向量组$a_{1}, a_{2}, \cdots, a_{m}$线性相关的充要条件是它所构成的矩阵$A=\left(a_{1}, a_{2}, \cdots, a_{m}\right)$的秩小于向量的个数m，及$R(A)<m$。

线性无关的充分必要条件是$R(A)=m$。

【定理3】若向量组$A: a_{1}, a_{2}, \cdots, a_{m}$线性相关，则向量组$B: a_{1}, a_{2}, \cdots, a_{m}, a_{m+1}$也线性相关；反言之，如果向量组B线性无关，则向量组A也线性无关。

• m个n维向量构成的向量组，当n<m时，一定线性相关。特别地，n+1个n维向量一定线性相关。

即一个向量组若有线性相关的部分组，则该向量组线性相关。特别地，含有零向量的向量组一定线性相关。反之，若一个向量组线性无关，则它的任何部分组都线性无关。

---

3 向量组的秩

3.1 最大线性无关向量组

【定义1】设有向量组A，若在A中能够选出r个向量$a_{1}, a_{2}, \cdots, a_{r}$，满足：

1. 向量组$A_0：a_{1}, a_{2}, \cdots, a_{r}$都线性无关
2. 向量组A中任意r+1个向量都线性相关

那么称向量组$A_0$是向量组A的一个最大线性无关向量组（简称最大无关组）。

最大无关组中所含向量的个数r称为向量组A的秩，记为$R_A$。

• 只含有零向量的向量组没有最大无关组，规定它的秩为0

3.2 矩阵的秩与向量组的秩

对于只含有限个向量的向量组$A：a_{1}, a_{2}, \cdots, a_{r}$，它可以构成矩阵$A=(a_{1}, a_{2}, \cdots, a_{m})$。

【定理1】矩阵的秩等于它的列向量组的秩，也等于它的行向量组的秩。

若$D_r$是矩阵A的一个最高阶非零子式：

1. $D_r$所在的r列是A的列向量组的一个最大无关组
2. $D_r$所在的r行是A的行向量组的一个最大无关组

说明：

1. 向量组的最大无关组不是唯一的
2. 向量组A与它的最大无关组$A_0$等价（向量组与其最大无关组可以相互表示）

3.3 总结

1. 最大线性无关向量组的概念——最大性、无关性
2. 矩阵的秩与向量组的秩之间的关系
3. 关于向量组秩的一些结论
4. 求向量组的秩及其最大无关组的方法
   • 将向量组中的向量作为列向量构成一个矩阵；
   • 对矩阵进行初等行变换化成行阶梯形矩阵，即可得到向量组的秩和最大无关组。

---

4 线性方程组的解的结构

4.1 齐次线性方程组的解的性质

【性质1】若$x=\xi_{1}$，$x=\xi_{2}$是齐次线性方程组的解，那么$x=\xi_1+\xi_2$也是方程的解。

【性质2】若$x=\xi_{1}$是齐次线性方程组的解，k为实数，那么$x=k\xi_1$也是方程的解。

4.2 基础解系及其求法

齐次线性方程组的解集的最大无关组称为该方程组的基础解系。

由上面讨论知，要求齐次线性方程组的通解，只需求出它的基础解系即可。

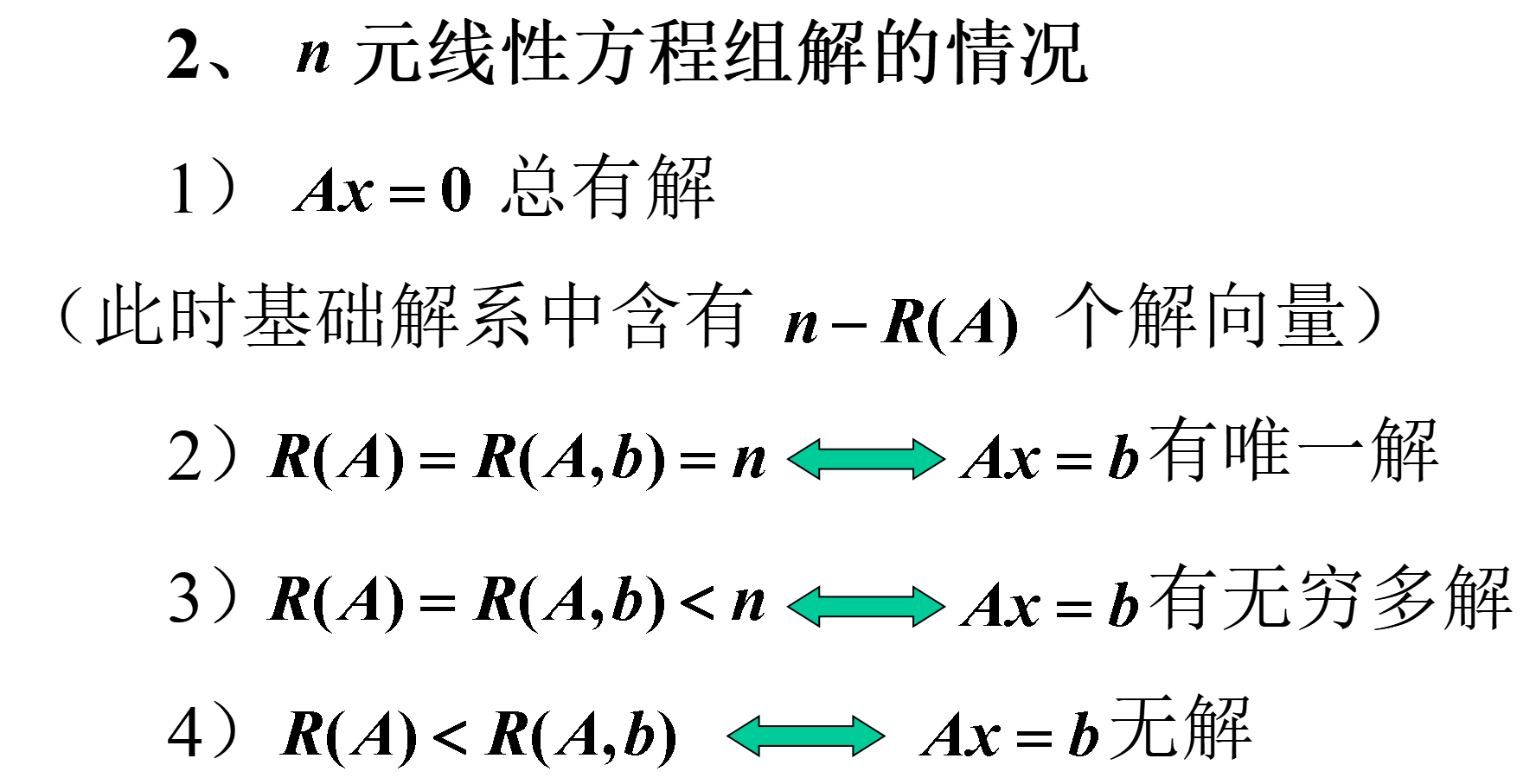
【定理1】设$m \times n$矩阵A的秩$R(A)=r$，则n元齐次线性方程组$Ax=0$的解集S的秩

$R_s=n-r$

• 当$R(A)=n$时，方程组只有零解，没有基础解系；
• 当$R(A)=r<n$时，方程组的基础解系中含有$n-r$个向量，此时任意$n-r$个线性无关的解均可构成它的基础解系，因此齐次线性方程组的基础解系不是唯一的，它的通解形式也不是唯一的。

4.3 非齐次线性方程组的解的性质

设有非齐次线性方程组

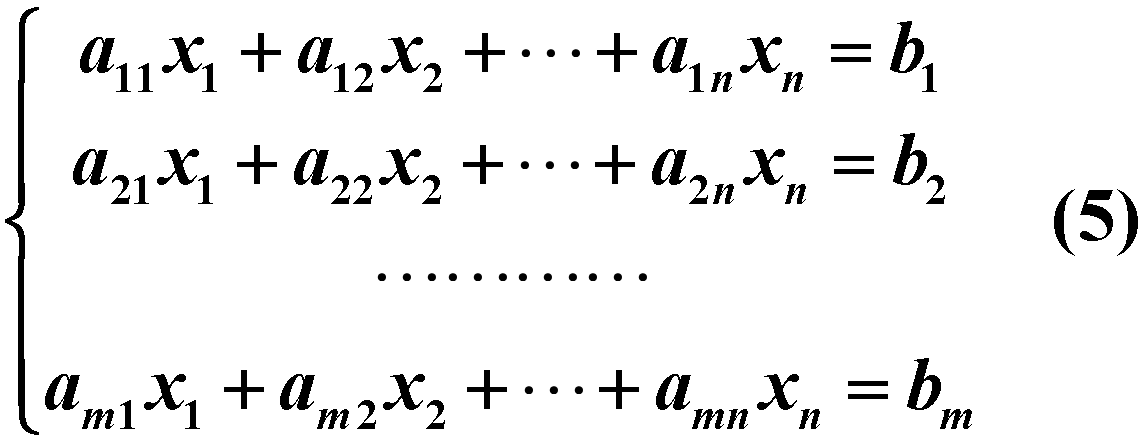
将其写成向量方程$Ax=b$，记为方程6。

【性质3】设$x=\eta_{1}$及$x=\eta_{2}$都是（6）的解，则$x=\eta_1 - \eta_2$为对应的齐次线性方程组$Ax=0$（记为方程7）的解。

【性质4】设$x=\eta$是方程（6）的解，$x=\xi$是方程（7）的解，则$x=\xi+\eta$仍是（6）的解。

非线性方程组的通解为

$x=k_1 \xi_1+k_{2} \xi_{2} + \cdots + k_{n-r} \xi_{n-r}+\eta^{*}$

其中$\xi_{1}, \xi_{2}, \cdots, \xi_{n-r}$是方程（7）的基础解系。

4.4 总结

---

5 向量空间

5.1 向量空间的概念

【定义1】设V是n维向量的集合，若集合V非空，且集合V对向量的加法及数乘两种运算封闭，那么称集合V为向量空间。

集合V对加法和数乘封闭是指

1. 若$\alpha \in V$，$\beta \in V$，则有$\alpha + \beta \in V$
2. 若$\alpha \in V$，$\lambda \in R$，则有$\lambda \alpha \in V$

n维向量的集合是一个向量空间，记作$R^n$。

一般地，由向量组$a_{1}, a_{2}, \cdots, a_{m}$生成的向量空间为

$L=\{x=\lambda_{1} a_{1}+\lambda_{2} a_{2}+\cdots+\lambda_{m} a_{m} \mid \lambda_{1}, \lambda_{2}, \cdots, \lambda_{m} \in \mathbb{R}\}$

5.2 向量空间的基与向量的坐标

【定义2】设V是向量空间，若存在r个向量$a_{1}, a_{2}, \cdots, a_{r} \in V$，且满足

1. $a_{1}, a_{2}, \cdots, a_{r}$线性无关
2. V中任一向量均可由$a_{1}, a_{2}, \cdots, a_{r}$线性表示

那么向量组$a_{1}, a_{2}, \cdots, a_{r}$就称为向量空间V的一个基，r称为向量空间V的维数，并称V为r维向量空间。

说明：

1. 只含有零向量的向量空间称为0维向量空间，因此它没有基。
2. 若将向量空间看成向量组，那么V的基就是向量组的最大无关组，V的维数就是向量组的秩。
3. 若向量组$a_1,a_2,...,a_r$是向量空间 V 的一个基，则 V 可以表示为

$V=\left\{x=\lambda_{1} a_{1}+\lambda_{2} a_{2}+\cdots+\lambda_{r} a_{r} \mid \lambda_{1}, \lambda_{2}, \cdots, \lambda_{r} \in \mathbb{R}\right\}$

即 V 是基所生成的向量空间，由此得出了向量空间 V 的构造方法。

例如，齐次线性方程组的解空间$S={x|Ax=0}$，若能找到解空间的一个基$\xi_{1}, \xi_{2}, \cdots, \xi_{n-r}$，则解空间为：

$S=\left\{x=c_{1} \xi_{1}+c_{2} \xi_{2}+\cdots+c_{n-r} \xi_{n-r} \mid c_{1}, c_{2}, \cdots, c_{n-r} \in \mathbb{R}\right\}$

【定义3】若在向量空间V中取定一个基$a_{1}, a_{2}, \cdots, a_{r}$，那么V中任意向量x可唯一标识为

$x=\lambda_{1} a_{1}+\lambda_{2} a_{2}+\cdots+\lambda_{r} a_{r}$

其中数组$\lambda_{1}, \lambda_{2}, \cdots, \lambda_{r}$称为x在基$a_{1}, a_{2}, \cdots, a_{r}$中的坐标。

特别地，在 n 维向量空间$R^n$中，取单位坐标向量组$e_1,e_2,...e_n$为基，则以$x_1,x_2,...,x_n$为分量的向量$x$可表示为：

$x=x_{1} e_{1}+x_{2} e_{2}+\cdots+x_{n} e_{n}$

可见向量在基$e_1,e_2,...e_n$中的坐标就是该向量的分量，因此$e_1,e_2,...e_n$称作$R^n$中的自然基。