1 数学期望

1.1 随机变量的数学期望概念

定义1：设$X$是离散型随机变量，它的分布律是：$P ( X=x_{k} ) =p_{k}, k=1,2, \ldots$，若级数$\sum_{k=1}^{\infty} x_{k} p_{k}$绝对收敛，则称级数$\sum_{k=1}^{\infty} x_{k} p_{k}$的和为随机变量$X$的数学期望。

$$
E(X)=\sum_{k=1}^{\infty} x_{k} p_{k}
$$

定义2：设连续型随机变量$X$的概率密度为$f(x)$，如果积分$\int_{-\infty}^{+\infty} x f(x) \mathrm{d} x$绝对收敛，则称该积分的值为随机变量X的数学期望或者均值，记为$E(X)$，即

$$
E(X)=\int_{-\infty}^{+\infty} x f(x) \mathrm{d} x
$$

1.2 随机变量函数的数学期望

定理1：设$Y$是随机变量$X$的函数$Y=g(X)$（ $g$ 是连续函数）：

当$X$为离散型时, 它的分布律为$P\left(X=x_{k}\right)=p_{k},(k=1,2, \ldots)$，若级数$\sum_{k=1}^{\infty} g\left(x_{k}\right) p_{k}$绝对收敛，则有：

$$
E(Y)=E[g(X)]=\sum_{k=1}^{\infty} g\left(x_{k}\right) p_{k}
$$

当X为连续型时, 它的密度函数为f(x)，若$\int_{-\infty}^{+\infty} g(x) f(x) d x$绝对收敛，则有：

$$
E(Y)=E[g(X)]=\int_{-\infty}^{+\infty} g(x) f(x) d x
$$

总结如下：

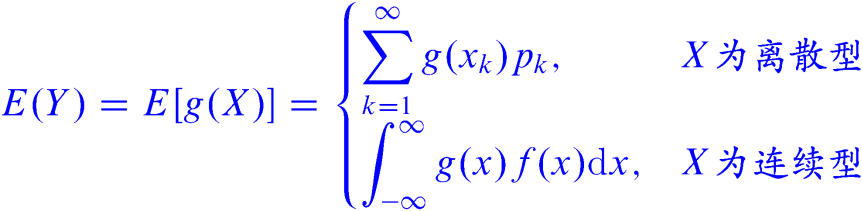
定理2：设$Z=g(X,Y)$ 是随机变量$X$、$Y$的函数，

(1) 如果X、Y是离散型随机变量，联合概率分布为pij , i,j=1,2, …，则

$$
E(Z)=E[g(X, Y)]=\sum_{i=1}^{\infty} \sum_{j=1}^{\infty} g\left(x_{i}, y_{j}\right) p_{i j}
$$

(2) 如果X、Y是连续型随机变量，联合概率密度为f(x,y)，则

$$
E(Z)=E[g(X, Y)]=\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} g(x, y) f(x, y) \mathrm{d} x \mathrm{~d} y
$$

1.3 数学期望的性质

设C是常数，则E(C)=C;
若k是常数，则E(kX)=kE(X);
E(X+Y) = E(X)+E(Y)，$推广 E\left[\sum_{i=1}^{n} X_{i}\right]=\sum_{i=1}^{n} E\left(X_{i}\right)$
设X、Y 相互独立，则 E(XY)=E(X)E(Y)，$推广 E\left[\prod_{i=1}^{n} X_{i}\right]=\prod_{i=1}^{n} E\left(X_{i}\right)$ ，诸 Xi相互独立时。

请注意：由E(XY)=E(X)E(Y)不一定能推出X,Y 独立。

1.4 小结

一维随机变量的数学期望：

离散型：$E(X)=\sum_{k=1}^{\infty} x_{k} p_{k}$
连续型：$E(X)=\int_{-\infty}^{+\infty} x f(x) \mathrm{d} x$

随机变量函数的数学期望：

一维函数

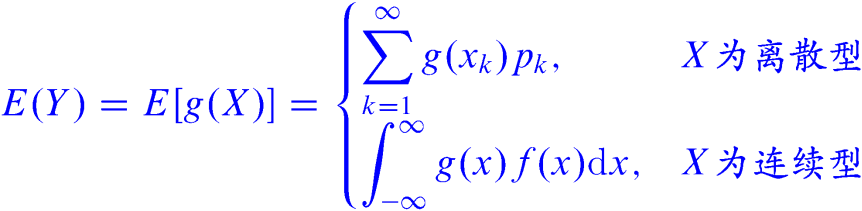
二维函数

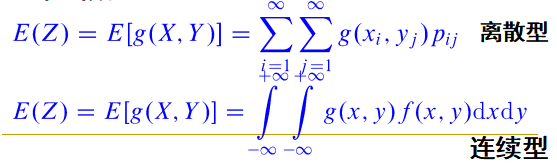
2 方差

2.1 方差的定义

方差是一个常用来体现随机变量取值分散程度的量。

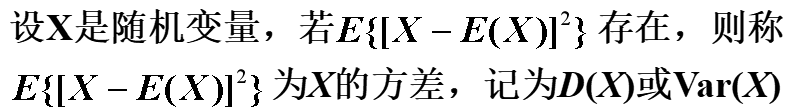
$$
D(X)=\mathrm{Var}(X)=E{[X-E(X)]^2}.
$$

称$\sqrt{D(X)}$为标准差或均方差，记为$\sigma(X)$。

2.2 方差的计算

2.2.1 利用定义计算

离散型：$D(X)=\sum_{k=1}^{+\infty}\left[x_k-E(X)\right]^2p_k,$其中$P{X=x_k}=p_k,k=1,2,\cdots,$是$X$的分布律。

连续性：$D(X)=\int_{-\infty}^{+\infty}[x-E(X)]^2f(x) \mathrm{d}x$，其中$f(x)$为$x$的概率密度。

2.2.2 利用公式计算

$$
D(X)=E(X^2)-[E(X)]^2.
$$

2.3 方差的性质

（1）设 C 是常数, 则有$D(C)=0$

（2）设 X 是一个随机变量, C 是常数, 则有$D(CX)=C^2D(X)$

（3）设 X, Y 相互独立, D(X), D(Y) 存在, 则$D(X\pm Y)=D(X)+D(Y).\quad D(X\pm C)=D(X).$

（4） D(X)=0的充要条件是X以概率1取常数E(X)，即$P{X=E(X)} = 1$

2.4 切比雪夫不等式

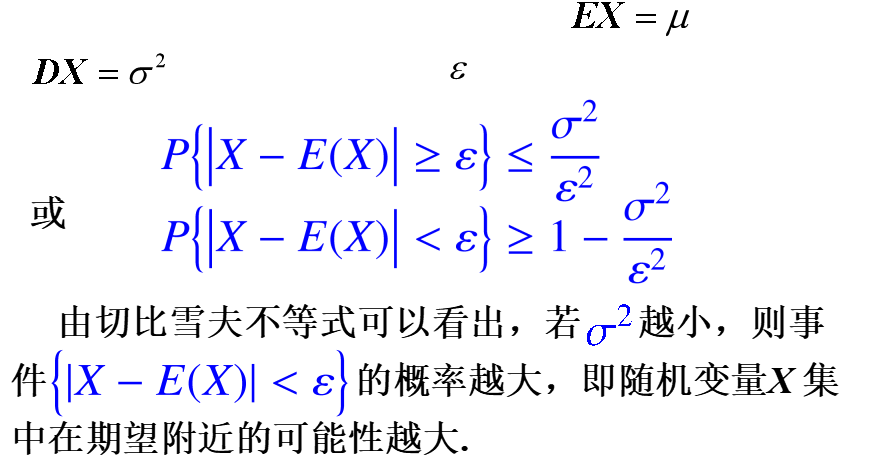
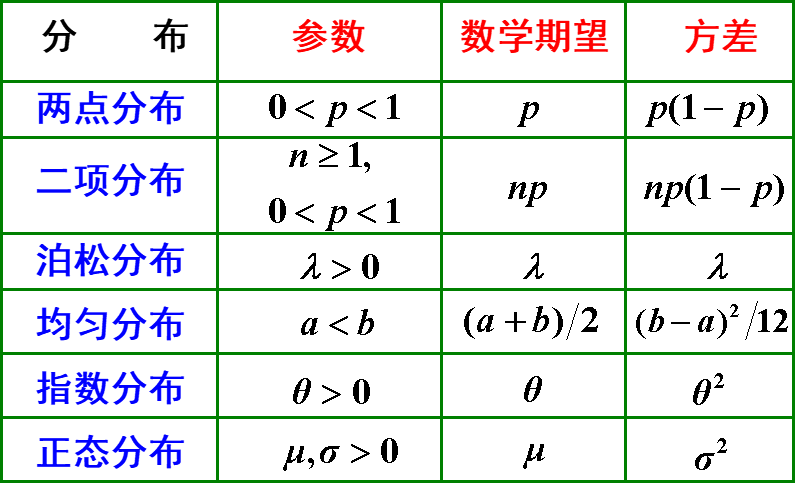
2.5 常见分布的期望与方差

3 协方差及相关系数

3.1 协方差

定义：量$E{[X-E(X)][Y-E(Y)]}$称为随机变量$X$和$Y$的协方差，记为$Cov(X,Y)$，即$\operatorname{Cov}(X, Y)=E{[X-E(X)][Y-E(Y)]}$。

计算协方差的一个简单公式：$\operatorname{Cov}(X, Y)=E(X Y)-E(X) E(Y)$

3.1.1 性质

$\operatorname{Cov}(X, C)=0, C 为常数$
$\operatorname{Cov}(X, X)=D(X)$
$\operatorname{Cov}(X, Y)=\operatorname{Cov}(Y, X)$
$\operatorname{Cov}\left(X_{1}+X_{2}, Y\right)=\operatorname{Cov}\left(X_{1}, Y\right)+\operatorname{Cov}\left(X_{2}, Y\right)$
$\operatorname{Cov}(a X, b Y)=a b \operatorname{Cov}(X, Y) \quad a, b 是常数$
$\operatorname{Cov}(a X+b, Y)=a \operatorname{Cov}(X, Y) \quad a, b 是常数$
$D(X \pm Y)=D(X)+D(Y) \pm 2 \operatorname{Cov}(X, Y)$
若$X$与$Y$独立，则$\operatorname{Cov}(X, Y)=0$