Python第5次作业
继续使用”数据12.1”,以总店数、年末从业人数、年末餐饮营业面积、统一配送商品购进额4个变量,即V2、V4、V5、V9,对所有样本观测值开展划分聚类分析和层次聚类分析。
- 载入分析所需要的库和模块
- 变量设置及数据处理
- 特征变量相关性分析
- 使用K均值聚类分析方法对样本示例进行聚类(K=2)
- 使用K均值聚类分析方法对样本示例进行聚类(K=3)
- 使用K均值聚类分析方法对样本示例进行聚类(K=4)
1. 载入分析所需要的库和模块
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler
2. 变量设置及数据处理
data = pd.read_csv('../data/数据12.1.csv')
X = data.iloc[:, [1,3,4,8]]
X.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 28 entries, 0 to 27
Data columns (total 4 columns):
# Column Non-Null Count Dtype
--- ------ -------------- ------
0 V2 28 non-null int64
1 V4 28 non-null float64
2 V5 28 non-null float64
3 V9 28 non-null float64
dtypes: float64(3), int64(1)
memory usage: 1.0 KB
数据共包含28个样本,4个特征变量。其中V2(总店数)为整数类型,V4(年末从业人数)、V5(年末餐饮营业面积)和V9(统一配送商品购进额)为浮点数类型。所有变量均无缺失值。
len(X.columns)
4
确认数据集包含4个特征变量,与作业要求一致。
X.columns
Index(['V2', 'V4', 'V5', 'V9'], dtype='object')
特征变量名称分别为V2、V4、V5、V9,对应题目要求的总店数、年末从业人数、年末餐饮营业面积和统一配送商品购进额。
X.shape
(28, 4)
数据集维度为28行4列,即28个样本观测值和4个特征变量。
X.dtypes
V2 int64
V4 float64
V5 float64
V9 float64
dtype: object
进一步确认各变量的数据类型,V2为整数型,其余三个变量为浮点型。
X.isnull().values.any()
np.False_
数据集不存在任何缺失值,返回结果为False。
X.isnull().sum()
V2 0
V4 0
V5 0
V9 0
dtype: int64
详细统计每个变量的缺失值数量,所有变量均无缺失值。
X.head(10)
| V2 | V4 | V5 | V9 | |
|---|---|---|---|---|
| 0 | 95 | 16.3 | 240.8 | 152.28 |
| 1 | 9 | 3.5 | 25.9 | 5.13 |
| 2 | 5 | 0.1 | 4.1 | 0.61 |
| 3 | 4 | 0.5 | 4.1 | 3.63 |
| 4 | 3 | 0.3 | 6.5 | 0.12 |
| 5 | 13 | 1.6 | 35.6 | 52.85 |
| 6 | 4 | 0.2 | 2.9 | 1.20 |
| 7 | 18 | 5.6 | 52.2 | 23.56 |
| 8 | 31 | 4.9 | 68.3 | 34.52 |
| 9 | 8 | 1.7 | 19.9 | 9.77 |
展示了数据集的前10个样本,可以观察到各变量的取值范围差异较大。例如,第一个样本(索引0)的V2(总店数)为95,远高于其他样本;V9(统一配送商品购进额)也显示出类似的数量级差异。
scaler = StandardScaler()
scaler.fit(X)
X_s = scaler.transform(X)
X_s = pd.DataFrame(X_s, columns=X.columns)
X_s
| V2 | V4 | V5 | V9 | |
|---|---|---|---|---|
| 0 | 3.331341 | 2.770017 | 3.405459 | 3.989002 |
| 1 | -0.373910 | 0.034349 | -0.259663 | -0.452757 |
| 2 | -0.546248 | -0.692313 | -0.631462 | -0.589194 |
| 3 | -0.589332 | -0.606824 | -0.631462 | -0.498035 |
| 4 | -0.632416 | -0.649569 | -0.590530 | -0.603985 |
| 5 | -0.201573 | -0.371727 | -0.094229 | 0.987683 |
| 6 | -0.589332 | -0.670941 | -0.651928 | -0.571385 |
| 7 | 0.013849 | 0.483169 | 0.188884 | 0.103557 |
| 8 | 0.573945 | 0.333562 | 0.463470 | 0.434387 |
| 9 | -0.416995 | -0.350355 | -0.361993 | -0.312698 |
| 10 | 0.229270 | -0.072514 | -0.269896 | -0.255044 |
| 11 | -0.589332 | -0.628196 | -0.597352 | -0.399631 |
| 12 | -0.029236 | -0.243493 | 0.035389 | -0.134303 |
| 13 | -0.158489 | -0.564079 | -0.553009 | -0.507091 |
| 14 | 0.703198 | 0.012976 | 0.158185 | 0.056770 |
| 15 | 0.013849 | 0.183955 | 0.214467 | -0.121625 |
| 16 | -0.589332 | -0.499962 | -0.566653 | -0.470868 |
| 17 | -0.718585 | -0.713686 | -0.696271 | -0.599156 |
| 18 | -0.244657 | 0.162583 | 0.402072 | -0.220029 |
| 19 | -0.330826 | 0.483169 | 0.224700 | -0.214897 |
| 20 | -0.675501 | -0.713686 | -0.672394 | -0.600967 |
| 21 | -0.546248 | -0.564079 | -0.605879 | -0.522183 |
| 22 | -0.718585 | -0.713686 | -0.699682 | -0.603080 |
| 23 | -0.330826 | -0.371727 | -0.430213 | -0.296699 |
| 24 | -0.632416 | -0.649569 | -0.665572 | -0.551463 |
| 25 | -0.546248 | -0.649569 | -0.633167 | -0.525202 |
| 26 | 1.952643 | 2.684527 | 2.279828 | 1.284706 |
| 27 | 2.641992 | 2.577665 | 2.238896 | 2.194187 |
通过StandardScaler将所有特征变量转换为均值为0、标准差为1的标准化数据。可以看到,第一个样本(索引0)的各项指标仍保持较高的标准化值(约2.77-3.99之间),而其他样本则分布在-0.7到0.7的范围内。标准化后的数据更适合进行聚类分析,可以避免因变量量级差异导致的聚类结果偏差。
3. 特征变量相关性分析
print(X_s.corr(method='pearson'))
V2 V4 V5 V9
V2 1.000000 0.946057 0.966842 0.938237
V4 0.946057 1.000000 0.977966 0.879125
V5 0.966842 0.977966 1.000000 0.938684
V9 0.938237 0.879125 0.938684 1.000000
相关性分析结果显示,所有特征变量之间存在高度正相关关系。相关系数均在0.87以上,其中V4和V5的相关系数最高(0.977966),表明年末从业人数和年末餐饮营业面积之间存在极强的线性关系。V2(总店数)与V5(年末餐饮营业面积)的相关系数也很高(0.966842)。
plt.subplot(1,1,1)
sns.heatmap(X_s.corr(), annot=True)
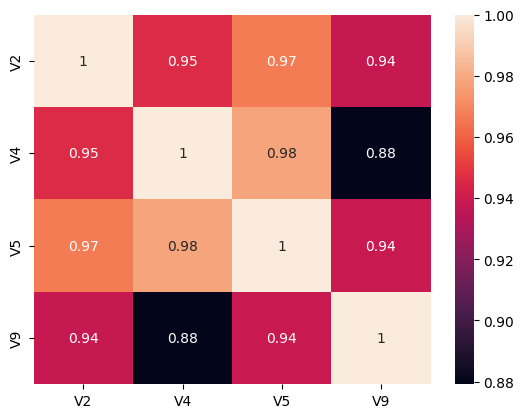
热力图直观展示了各变量间的相关系数。颜色深浅表示相关程度,越接近红色表示相关性越强。图中对角线为自相关系数1,其他格子中的数字即为相关系数值。
4. K均值聚类分析
4.1 对样本示例进行聚类(K=2)
model = KMeans(n_clusters=2, random_state=2)
model.fit(X_s)
model.labels_
array([1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 1, 1], dtype=int32)
使用K=2的K均值聚类算法完成了对28个样本的聚类。结果显示,大部分样本(25个)被分到第0类,只有3个样本(索引0、26、27)被分到第1类。这表明数据中存在明显的少数离群点或特殊群体。
pd.DataFrame(model.labels_.T, index=data.V1,columns=['聚类'])
| 聚类 | |
|---|---|
| V1 | |
| 北京 | 1 |
| 天津 | 0 |
| 河北 | 0 |
| 山西 | 0 |
| 内蒙古 | 0 |
| 辽宁 | 0 |
| 黑龙江 | 0 |
| 江苏 | 0 |
| 浙江 | 0 |
| 安徽 | 0 |
| 福建 | 0 |
| 江西 | 0 |
| 山东 | 0 |
| 河南 | 0 |
| 湖北 | 0 |
| 湖南 | 0 |
| 广西 | 0 |
| 海南 | 0 |
| 重庆 | 0 |
| 四川 | 0 |
| 贵州 | 0 |
| 云南 | 0 |
| 西藏 | 0 |
| 陕西 | 0 |
| 甘肃 | 0 |
| 新疆 | 0 |
| 上海 | 1 |
| 广东 | 1 |
按省份名称显示聚类结果,可以清晰看到第1类包含北京、上海和广东三个地区,其他25个地区属于第0类。这表明在商业规模(总店数、从业人数、营业面积和配送额)方面,北京、上海和广东明显领先于其他地区,形成了一个高规模的特殊群体。
model.cluster_centers_
array([[-0.31703902, -0.32128836, -0.31696734, -0.29871581],
[ 2.64199186, 2.67740299, 2.64139452, 2.48929838]])
展示了两个聚类中心的坐标。第0类的中心坐标全部为负值,而第1类的中心坐标全部为较大的正值(约2.49-2.68之间)。这进一步证实了两类之间存在显著差异,第1类(北京、上海、广东)在所有标准化特征上都远高于平均水平,而第0类则略低于平均水平。
model.inertia_
20.197477847186683
聚类的惯性(inertia)值为20.197,这是各样本到其所属聚类中心距离的平方和。该值反映了聚类的紧密程度,值越小表示聚类效果越好。
4.2 对样本示例进行聚类(K=3)
model = KMeans(n_clusters=3, random_state=2)
model.fit(X_s)
model.labels_
array([1, 0, 2, 2, 2, 0, 2, 0, 0, 2, 0, 2, 0, 2, 0, 0, 2, 2, 0, 0, 2, 2, 2, 2, 2, 2, 1, 1], dtype=int32)
使用K=3的K均值聚类算法完成了聚类。结果显示,样本被分为三类,其中第2类数量最多(15个样本),第0类次之(9个样本),第1类最少(4个样本)。
pd.DataFrame(model.labels_.T, index=data.V1,columns=['聚类'])
| 聚类 | |
|---|---|
| V1 | |
| 北京 | 1 |
| 天津 | 0 |
| 河北 | 2 |
| 山西 | 2 |
| 内蒙古 | 2 |
| 辽宁 | 0 |
| 黑龙江 | 2 |
| 江苏 | 0 |
| 浙江 | 0 |
| 安徽 | 2 |
| 福建 | 0 |
| 江西 | 2 |
| 山东 | 0 |
| 河南 | 2 |
| 湖北 | 0 |
| 湖南 | 0 |
| 广西 | 2 |
| 海南 | 2 |
| 重庆 | 0 |
| 四川 | 0 |
| 贵州 | 2 |
| 云南 | 2 |
| 西藏 | 2 |
| 陕西 | 2 |
| 甘肃 | 2 |
| 新疆 | 2 |
| 上海 | 1 |
| 广东 | 1 |
按省份显示的聚类结果显示了更细致的分类:
- 第1类:北京、上海、广东(3个地区)- 商业规模最大
- 第0类:天津、辽宁、江苏、浙江、福建、山东、湖北、湖南、重庆、四川(9个地区)- 商业规模中等
- 第2类:河北、山西、内蒙古、黑龙江、安徽、江西、河南、广西、海南、贵州、云南、西藏、陕西、甘肃、新疆(15个地区)- 商业规模较小
这种分类反映了各地区商业发展的梯度特征,经济发达地区(如北京、上海、广东)明显领先,部分沿海和中部地区次之,西部和东北地区相对落后。
np.set_printoptions(suppress=True)
model.cluster_centers_
array([[ 0.03539069, 0.10060298, 0.10633798, 0.01837419],
[ 2.64199186, 2.67740299, 2.64139452, 2.48929838],
[-0.55199216, -0.60254925, -0.59917089, -0.51010914]])
三个聚类中心的坐标清晰地展示了梯度差异:
- 第1类中心:所有特征的标准化值均在2.4-2.7之间,远高于平均值
- 第0类中心:所有特征的标准化值接近0(约0.02-0.11之间),接近全国平均水平
- 第2类中心:所有特征的标准化值均为负值(约-0.51到-0.60之间),低于全国平均水平
model.inertia_
10.498603411717772
当K=3时,聚类的惯性值为10.499,比K=2时的20.197显著降低。这表明增加聚类数量有助于减小类内差异,提高聚类的紧密程度。
4.3 对样本示例进行聚类(K=4)
model = KMeans(n_clusters=4, random_state=3)
model.fit(X_s)
model.labels_
array([3, 0, 2, 2, 2, 0, 2, 0, 0, 2, 0, 2, 0, 2, 0, 0, 2, 2, 0, 0, 2, 2, 2, 2, 2, 2, 1, 1], dtype=int32)
使用K=4的K均值聚类算法完成了聚类。结果显示,样本被分为四类,其中第2类数量最多(15个样本),第0类次之(9个样本),第1类和第3类各有2个样本。
pd.DataFrame(model.labels_.T, index=data.V1,columns=['聚类'])
| 聚类 | |
|---|---|
| V1 | |
| 北京 | 3 |
| 天津 | 0 |
| 河北 | 2 |
| 山西 | 2 |
| 内蒙古 | 2 |
| 辽宁 | 0 |
| 黑龙江 | 2 |
| 江苏 | 0 |
| 浙江 | 0 |
| 安徽 | 2 |
| 福建 | 0 |
| 江西 | 2 |
| 山东 | 0 |
| 河南 | 2 |
| 湖北 | 0 |
| 湖南 | 0 |
| 广西 | 2 |
| 海南 | 2 |
| 重庆 | 0 |
| 四川 | 0 |
| 贵州 | 2 |
| 云南 | 2 |
| 西藏 | 2 |
| 陕西 | 2 |
| 甘肃 | 2 |
| 新疆 | 2 |
| 上海 | 1 |
| 广东 | 1 |
按省份显示的K=4聚类结果进一步细分了高规模群体:
- 第3类:仅北京(1个地区)- 商业规模最高
- 第1类:上海、广东(2个地区)- 商业规模次高
- 第0类:天津、辽宁、江苏、浙江、福建、山东、湖北、湖南、重庆、四川(9个地区)- 商业规模中等
- 第2类:河北、山西、内蒙古、黑龙江、安徽、江西、河南、广西、海南、贵州、云南、西藏、陕西、甘肃、新疆(15个地区)- 商业规模较小
这种分类将北京单独列为一类,表明北京在商业规模方面可能具有独特的领先地位,与上海和广东也存在一定差距。
model.cluster_centers_
array([[ 0.03539069, 0.10060298, 0.10633798, 0.01837419],
[ 2.29731732, 2.6310961 , 2.25936232, 1.7394465 ],
[-0.55199216, -0.60254925, -0.59917089, -0.51010914],
[ 3.33134093, 2.77001676, 3.40545892, 3.98900215]])
四个聚类中心的坐标详细展示了商业规模的梯度差异:
- 第3类中心(北京):所有特征的标准化值都非常高,尤其是V9(统一配送商品购进额)达到3.99,显著高于其他地区
- 第1类中心(上海、广东):所有特征的标准化值也较高(1.74-2.63之间),但低于北京
- 第0类中心:所有特征的标准化值接近0,保持在平均水平
- 第2类中心:所有特征的标准化值均为负值,低于平均水平
这种细分结果更好地反映了不同发达地区之间的差异。
model.inertia_
5.523575558087604
当K=4时,聚类的惯性值进一步降低至5.524,相比K=3时的10.499又减少了近一半。这表明增加聚类数量确实能提高聚类的紧密程度。从结果来看,K=4的聚类能够更细致地区分不同规模的商业群体。