Python 第4次作业
使用”数据6.1”数据文件(详情已在第6章中介绍),以收入档次 (V1)为响应变量,以工作年限(V2)、绩效考核得分(V3)和违规操作积 分(V4)为特征变量,构建判别分析算法模型。
1. 载入分析所需要的模块和函数
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.metrics import confusion_matrix
from sklearn.metrics import classification_report
from sklearn.metrics import cohen_kappa_score
2. 数据读取及观察
data = pd.read_csv('../data/数据6.1.csv')
data.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 1034 entries, 0 to 1033
Data columns (total 5 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 V1 1034 non-null int64
1 V2 1034 non-null int64
2 V3 1034 non-null float64
3 V4 1034 non-null float64
4 V5 1034 non-null int64
dtypes: float64(2), int64(3)
memory usage: 40.5 KB
数据加载成功,共包含1034个样本,5个变量。其中V1(收入档次)、V2(工作年限)和V5为整数类型,V3(绩效考核得分)和V4(违规操作积分)为浮点类型。所有变量均无缺失值。
len(data.columns)
5
数据集共有5个变量列。
data.columns
Index(['V1', 'V2', 'V3', 'V4', 'V5'], dtype='object')
显示了数据集中所有变量的名称,分别为V1、V2、V3、V4和V5。
data.shape
(1034, 5)
数据形状为1034行5列,与之前的信息一致,确认样本数量和变量数量。
data.dtypes
V1 int64
V2 int64
V3 float64
V4 float64
V5 int64
dtype: object
详细列出了每个变量的数据类型,V1、V2、V5为整数类型,V3、V4为浮点类型。
data.isnull().values.any()
np.False_
检查数据中是否存在缺失值,返回结果为False,表明整个数据集中没有任何缺失值。
data.isnull().sum()
V1 0
V2 0
V3 0
V4 0
V5 0
dtype: int64
具体计算每个变量中的缺失值数量,所有变量的缺失值计数均为0,再次确认数据完整性。
data.head()
| V1 | V2 | V3 | V4 | V5 | |
|---|---|---|---|---|---|
| 0 | 3 | 2 | 110.9 | 107.0 | 2 |
| 1 | 3 | 5 | 73.8 | 73.5 | 2 |
| 2 | 3 | 2 | 111.3 | 101.9 | 2 |
| 3 | 3 | 4 | 247.7 | 202.0 | 2 |
| 4 | 3 | 8 | 227.5 | 167.0 | 2 |
显示了数据的前5行记录,从中可以观察到各变量的具体数值。例如,前5条记录的V1值均为3,表示这些样本的收入档次为3(低收入)。
data.V1.value_counts()
V1
2 417
3 407
1 210
Name: count, dtype: int64
统计了响应变量V1(收入档次)的分布情况。数据集中,收入档次为2(中收入)的样本最多,有417个;档次为3(低收入)的样本次之,有407个;档次为1(高收入)的样本最少,有210个。
3. 特征变量相关性分析
X = data.drop(['V1', 'V5'], axis=1) # 设置特征变量,即除V1之外的全部变量
y = data['V1'] # 设置响应变量,即V1
X.corr()
| V2 | V3 | V4 | |
|---|---|---|---|
| V2 | 1.000000 | 0.265740 | 0.089397 |
| V3 | 0.265740 | 1.000000 | 0.820136 |
| V4 | 0.089397 | 0.820136 | 1.000000 |
计算并显示了特征变量V2、V3、V4之间的相关系数矩阵。V3和V4之间存在高度正相关(相关系数为0.820136),而V2与V3、V4的相关性较低。
sns.heatmap(X.corr(), cmap='Blues', annot=True)
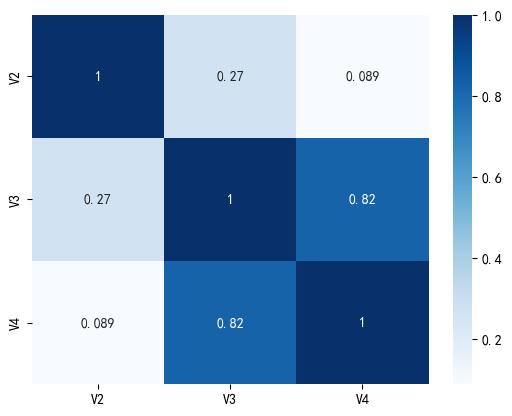
通过热力图可视化了特征变量之间的相关性。图中颜色深浅表示相关程度,数值标注了具体的相关系数。可以直观地看到V3和V4之间的强相关性。
4. 使用样本示例全集开展线性判别分析
4.1 模型估计及性能分析
# 使用LDA算法
model = LinearDiscriminantAnalysis()
model.fit(X, y)
model.score(X, y)
0.941972920696325
创建并训练了LDA模型,在训练集上的准确率为94.20%,表明模型对训练数据的分类效果良好。
model.priors_
array([0.20309478, 0.4032882 , 0.39361702])
显示了模型估计的先验概率,分别对应收入档次1、2、3的先验概率,约为20.31%、40.33%和39.36%,与样本中的实际分布基本一致。
model.means_
array([[ 26.77619048, 201.27952381, 148.29857143],
[ 17.75539568, 151.67577938, 129.18153477],
[ 6.36855037, 151.31498771, 134.27665848]])
显示了每个收入档次的特征变量均值。第一行是高收入群体(V1=1)的均值,第二行是中收入群体(V1=2)的均值,第三行是低收入群体(V1=3)的均值。可以看出不同收入档次在工作年限(V2)上的均值差异较大。
np.set_printoptions(suppress=True)
# 输出模型系数
model.coef_
array([[ 0.82747483, 0.03041262, -0.02576049],
[ 0.19186874, -0.00554052, 0.00173484],
[-0.62353557, -0.01001536, 0.01151419]])
显示了LDA模型的系数矩阵,每一行对应一个类别(收入档次)的判别函数系数。例如,第一行是区分高收入与其他收入档次的系数。
# 输出模型截距项
model.intercept_
array([-20.79039778, -3.42192464, 5.77888113])
显示了LDA模型的截距项,与系数矩阵对应,每一行一个截距值。
# 输出可解释方差比例
model.explained_variance_ratio_
array([0.98306151, 0.01693849])
显示了LDA投影后的两个判别分量解释的方差比例。第一个判别分量(LD1)解释了98.31%的方差,第二个判别分量(LD2)仅解释了1.69%的方差,说明数据的主要差异可以通过第一个判别分量来表示。
model.scalings_
array([[-0.26211658, -0.05094088],
[-0.00620112, 0.02973706],
[ 0.00605892, -0.01776271]])
显示了LDA模型的缩放因子矩阵,用于将原始特征空间投影到判别空间。
lda_scores = model.fit(X, y).transform(X)
lda_scores.shape
(1034, 2)
将原始特征数据投影到LDA判别空间,得到1034个样本在两个判别分量上的得分,形状为(1034, 2)。
lda_scores[:5, :]
array([[ 3.57952136, -0.34171335],
[ 2.82025903, -1.00273009],
[ 3.5461404 , -0.23922872],
[ 2.78257341, 1.936977 ],
[ 1.64730727, 1.75421967]])
显示了前5个样本的LDA判别得分,每个样本有两个得分值,分别对应LD1和LD2。
LDA_scores = pd.DataFrame(lda_scores, columns=['LD1', 'LD2'])
LDA_scores['收入档次'] = data['V1']
LDA_scores.head()
| LD1 | LD2 | 收入档次 | |
|---|---|---|---|
| 0 | 3.579521 | -0.341713 | 3 |
| 1 | 2.820259 | -1.002730 | 3 |
| 2 | 3.546140 | -0.239229 | 3 |
| 3 | 2.782573 | 1.936977 | 3 |
| 4 | 1.647307 | 1.754220 | 3 |
将LDA判别得分与原始收入档次合并为一个DataFrame,方便后续可视化分析。前5个样本的收入档次均为3(低收入)。
d = {1: '高收入', 2: '中收入', 3: '低收入'}
LDA_scores['收入档次'] = LDA_scores['收入档次'].map(d)
LDA_scores.head()
| LD1 | LD2 | 收入档次 | |
|---|---|---|---|
| 0 | 3.579521 | -0.341713 | 低收入 |
| 1 | 2.820259 | -1.002730 | 低收入 |
| 2 | 3.546140 | -0.239229 | 低收入 |
| 3 | 2.782573 | 1.936977 | 低收入 |
| 4 | 1.647307 | 1.754220 | 低收入 |
将收入档次的数值标签(1、2、3)映射为文字标签(高收入、中收入、低收入),使数据更易于理解。
# 解决图表中负号不显示问题
plt.rcParams['axes.unicode_minus'] = False
# 解决图表中中文显示问题
plt.rcParams['font.sans-serif'] = ['SimHei']
sns.scatterplot(x='LD1', y='LD2', data=LDA_scores, hue='收入档次')
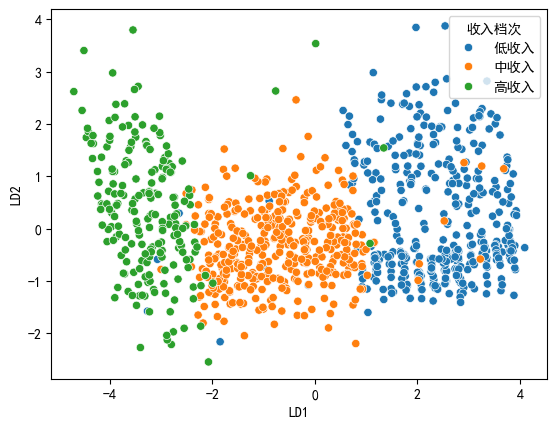
绘制了LDA判别得分的散点图,不同颜色表示不同的收入档次。从图中可以看出,三个收入档次在LDA判别空间中大致可以区分开,其中LD1(水平轴)是主要的区分维度。
4.2 运用两个特征变量绘制LDA决策边界图
!pip --default-timeout=123 install mlxtend
Requirement already satisfied: mlxtend in /opt/miniconda3/lib/python3.13/site-packages (0.23.4)
Requirement already satisfied: scipy>=1.2.1 in /opt/miniconda3/lib/python3.13/site-packages (from mlxtend) (1.16.1)
Requirement already satisfied: numpy>=1.16.2 in /opt/miniconda3/lib/python3.13/site-packages (from mlxtend) (2.3.2)
Requirement already satisfied: pandas>=0.24.2 in /opt/miniconda3/lib/python3.13/site-packages (from mlxtend) (2.3.3)
Requirement already satisfied: scikit-learn>=1.3.1 in /opt/miniconda3/lib/python3.13/site-packages (from mlxtend) (1.7.1)
Requirement already satisfied: matplotlib>=3.0.0 in /opt/miniconda3/lib/python3.13/site-packages (from mlxtend) (3.10.7)
Requirement already satisfied: joblib>=0.13.2 in /opt/miniconda3/lib/python3.13/site-packages (from mlxtend) (1.5.1)
Requirement already satisfied: contourpy>=1.0.1 in /opt/miniconda3/lib/python3.13/site-packages (from matplotlib>=3.0.0->mlxtend) (1.3.3)
Requirement already satisfied: cycler>=0.10 in /opt/miniconda3/lib/python3.13/site-packages (from matplotlib>=3.0.0->mlxtend) (0.12.1)
Requirement already satisfied: fonttools>=4.22.0 in /opt/miniconda3/lib/python3.13/site-packages (from matplotlib>=3.0.0->mlxtend) (4.60.1)
Requirement already satisfied: kiwisolver>=1.3.1 in /opt/miniconda3/lib/python3.13/site-packages (from matplotlib>=3.0.0->mlxtend) (1.4.9)
Requirement already satisfied: packaging>=20.0 in /opt/miniconda3/lib/python3.13/site-packages (from matplotlib>=3.0.0->mlxtend) (24.2)
Requirement already satisfied: pillow>=8 in /opt/miniconda3/lib/python3.13/site-packages (from matplotlib>=3.0.0->mlxtend) (11.3.0)
Requirement already satisfied: pyparsing>=3 in /opt/miniconda3/lib/python3.13/site-packages (from matplotlib>=3.0.0->mlxtend) (3.2.5)
Requirement already satisfied: python-dateutil>=2.7 in /opt/miniconda3/lib/python3.13/site-packages (from matplotlib>=3.0.0->mlxtend) (2.9.0.post0)
Requirement already satisfied: pytz>=2020.1 in /opt/miniconda3/lib/python3.13/site-packages (from pandas>=0.24.2->mlxtend) (2025.2)
Requirement already satisfied: tzdata>=2022.7 in /opt/miniconda3/lib/python3.13/site-packages (from pandas>=0.24.2->mlxtend) (2025.2)
Requirement already satisfied: six>=1.5 in /opt/miniconda3/lib/python3.13/site-packages (from python-dateutil>=2.7->matplotlib>=3.0.0->mlxtend) (1.17.0)
Requirement already satisfied: threadpoolctl>=3.1.0 in /opt/miniconda3/lib/python3.13/site-packages (from scikit-learn>=1.3.1->mlxtend) (3.6.0)
安装了mlxtend库,该库提供了绘制决策边界的功能。由于已经安装过,所以显示”Requirement already satisfied”。
from mlxtend.plotting import plot_decision_regions#导入plot_decision_regions
从mlxtend库中导入了plot_decision_regions函数,用于绘制分类模型的决策边界。
X2 = X.iloc[:, 0:2] # 仅选取V2存款规模、V3EVA作为特征变量
model = LinearDiscriminantAnalysis() # 使用LDA算法
model.fit(X2, y)
model.score(X2, y)
0.9410058027079303
仅使用V2和V3两个特征变量重新训练了LDA模型,模型在训练集上的准确率为94.10%,与使用全部三个特征变量的效果接近。
model.explained_variance_ratio_
array([0.98603802, 0.01396198])
仅使用两个特征变量时,LDA的第一个判别分量解释了98.60%的方差,第二个判别分量解释了1.40%的方差,与使用三个特征变量的情况类似。
plot_decision_regions(np.array(X2), np.array(y), model)
plt.xlabel('存款规模')#将x轴设置为'存款规模'
plt.ylabel('EVA')#将y轴设置为'EVA'
plt.title('LDA决策边界')#将标题设置为'LDA决策边界'
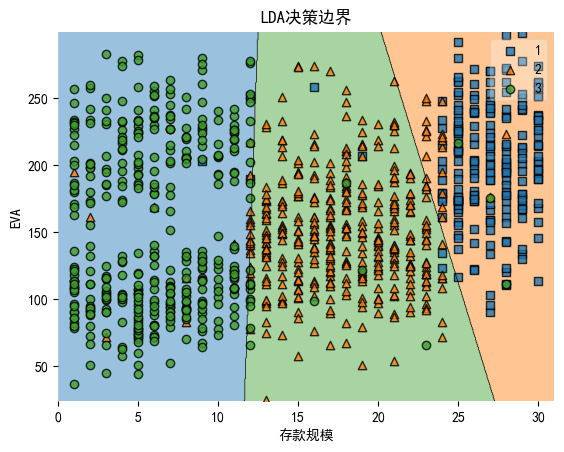
绘制了LDA模型在V2(存款规模)和V3(EVA)两个特征变量上的决策边界图。图中不同颜色区域表示不同收入档次的分类区域,圆点表示样本点。决策边界将特征空间划分为三个区域,分别对应高收入、中收入和低收入三个类别。
5. 使用分割样本开展线性判别分析
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.3, stratify=y, random_state=123)
model = LinearDiscriminantAnalysis()
model.fit(X_train, y_train)
model.score(X_test, y_test)
0.9742765273311897
将数据集按7:3的比例分割为训练集和测试集,并保持了原始的类别分布(stratify=y)。在训练集上训练LDA模型后,在测试集上的准确率达到了97.43%,表明模型具有良好的泛化能力。
prob = model.predict_proba(X_test)
prob[:5]
array([[0.02195931, 0.92653898, 0.05150171],
[0.03569766, 0.9598369 , 0.00446544],
[0.00115299, 0.57214367, 0.42670334],
[0. , 0.00039815, 0.99960185],
[0.98726864, 0.01273121, 0.00000015]])
获取了模型对测试集中前5个样本的概率预测。每行的三个数值分别表示样本属于高收入、中收入和低收入的概率。例如,第一个样本有92.65%的概率属于中收入。
pred = model.predict(X_test)
pred[:5]
array([2, 2, 2, 3, 1])
获取了模型对测试集中前5个样本的类别预测结果。预测结果分别为2(中收入)、2(中收入)、2(中收入)、3(低收入)和1(高收入)。
confusion_matrix(y_test, pred)#输出测试样本的混淆矩阵
array([[ 60, 2, 1],
[ 0, 121, 5],
[ 0, 0, 122]])
生成了测试集的混淆矩阵。混淆矩阵的行表示实际类别,列表示预测类别。从矩阵可以看出:
- 高收入(1)类:60个样本被正确预测,2个被错误预测为中收入,1个被错误预测为低收入
- 中收入(2)类:121个样本被正确预测,5个被错误预测为低收入
- 低收入(3)类:122个样本全部被正确预测
print(classification_report(y_test, pred))
precision recall f1-score support
1 1.00 0.95 0.98 63
2 0.98 0.96 0.97 126
3 0.95 1.00 0.98 122
accuracy 0.97 311
macro avg 0.98 0.97 0.97 311
weighted avg 0.98 0.97 0.97 311
输出了详细的分类报告,包括精确率(precision)、召回率(recall)、F1分数(f1-score)和支持样本数(support)。所有类别的精确率和召回率都很高(>95%),F1分数也都在0.97以上,表明模型分类效果非常好。
cohen_kappa_score(y_test, pred)
0.9597586814822003
计算了Cohen’s Kappa系数,值为0.9598,接近于1,表明模型的分类结果与实际类别之间有极高的一致性,远好于随机分类的结果。