编译原理第6章:自底向上的语法分析
1 自底向上分析概述从分析树的底部(叶节点)向顶部(根节点)方向构造分析树,可以看成是将输入串w归约为文法开始符号S的过程。
自顶向下的语法分析采用最左推导方式
自底向上的语法分析采用最左归约方式(反向构造最右推导)
自底向上语法分析的通用框架:移入-归约分析(Shift-Reduce Parsing)。
1.1 移入-归约分析的工作过程在对输入串的一次从左到右扫描过程中,语法分析器将零个或多个输入符号移入到栈的顶端,直到它可以对栈顶的一个文法符号串β进行归约为止。
然后,它将β归约为某个产生式的左部,语法分析器不断地重复这个循环,直到它检测到一个语法错误,或者栈中包含了开始符号且输入缓冲区为空(当出现这种情况时,语法分析器停止运行,并宣称成功完成了语法分析)为止。
1.2 移入-归约分析器可采取的4种动作
移入:将下一个输入符号移到栈的顶端
归约:被归约的符号串的右端必然处于栈顶。语法分析器在栈中确定这个串的左端,并决定用哪个非终结符来替换这个串
接收:宣布语法分析过程成功完成
报错:发现一个语法错误,并调用错误恢复子例程
移入-归约分析中存在的问题:如何正确地识别句柄?
...
编译原理第4章:自顶向下的语法分析
1 自顶向下分析概述
从分析树的顶部(根节点)向底部(叶节点)方向构造分析树,可以看成是从文法开始符号$S$推导出词串$w$的过程。
每一步推导中,都需要做两个选择:
替换当前句型中的哪个非终结符
用该非终结符的哪个候选式进行替换
1.1 最左推导在最左推导中,总是选择每个句型的最左非终结符进行替换。
如果$\boldsymbol{S} \Rightarrow{ }_{l m}^{*} \boldsymbol{\alpha}$,则称$\alpha$是当前文法的最左句型(left-sentential form)。
1.2 最右推导在最右推导中,总是选择每个句型的最右非终结符进行替换。
在自底向上的分析中,总是采用最左归约的方式,因此把最左归约称为规范归约,而最右推导相应地称为规范推导。
1.3 最左推导和最右推导的唯一性
如果最左推导和最右推导生成的语法树不是唯一的,那么这个文法就有二义性。
1.3.1 自顶向下的语法分析采用最左推导方式
总是选择每个句型的最左非终结符进行替换
根据输入流中的下一个终结符,选择最左非终结符的一个候选式
1.4 自顶向下语法分析的通用形式1 ...
编译原理第3章:词法分析
1 词法分析程序的设计1.1 词法分析流程逐个读入源程序字符并按照构词规则切分成一系列单词(token)。
单词是语言中具有独立意义的最小单位,包括保留关键字、标识符、常量、运算符、标点符号、分界符等。
词法分析是编译过程中的一个阶段,在语法分析前进行,也可和语法分析结合在一起作为一遍,由语法分析程序调用词法分析程序来获得当前单词供语法分析使用。
词法分析程序的主要任务及输出:
读源程序,产生用二元组表示的单词符号
滤掉空格,跳过注释、换行符
记录源程序的行号,以便出错处理程序准确定位源程序的错误
宏展开等…
2 正则表达式
正则表达式(Regular Expression,RE)是一种用来描述正则语言的更紧凑的表示方法。
例如:$r = a (a \mid b)^* (\varepsilon \mid(. \mid \_ )(a \mid b)(a \mid b)^*)$
正则表达式可以由较小的正则表达式按照特定规则递归地构建。每个正则表达式 $r$ 定义(表示)一个语言,记为$L(r)$。
这个语言也是根据 $r$ 的子表达式所表示的语言递归定义的。
2.1 ...
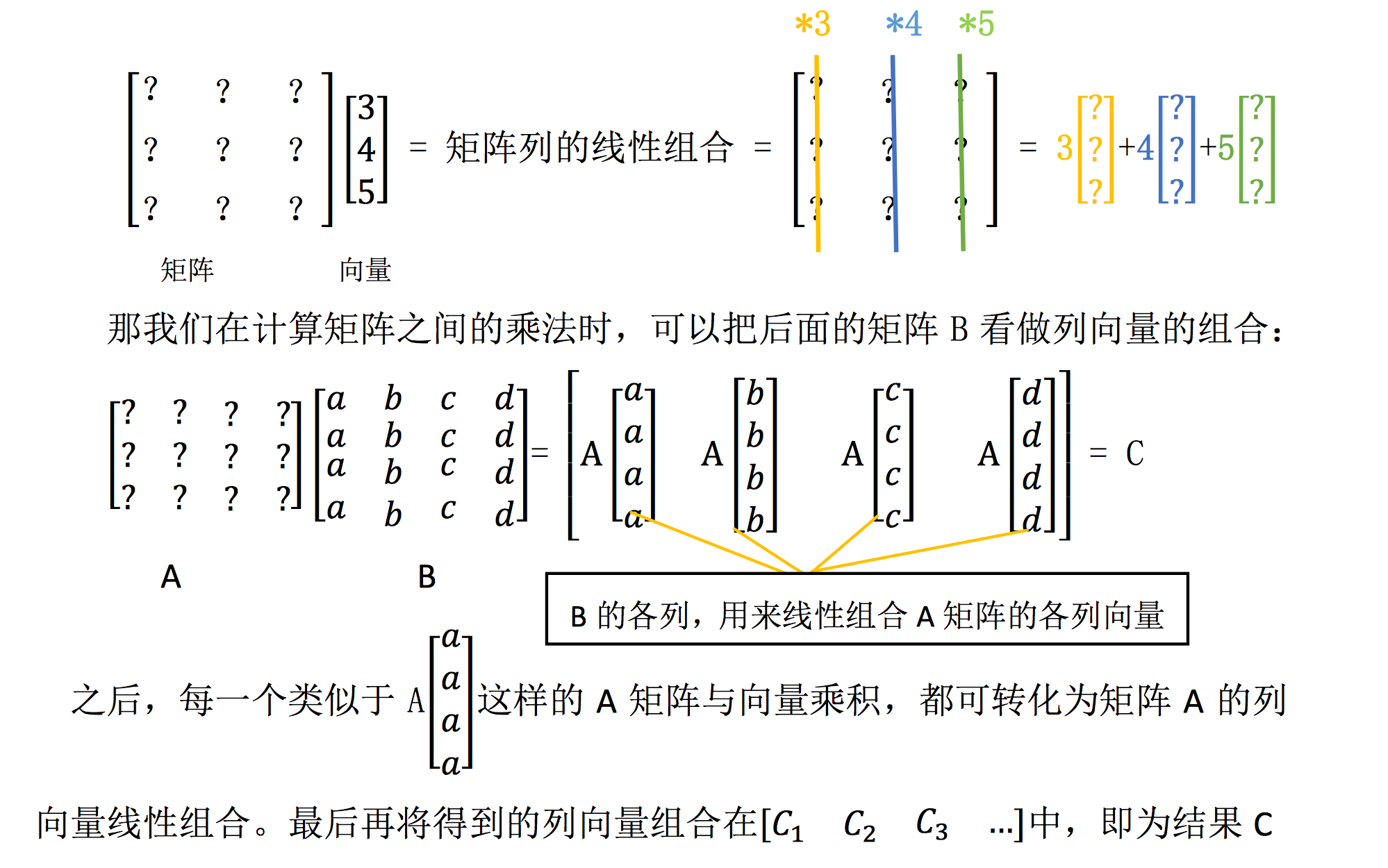
线性代数第4章:向量组的线性相关性
1 向量组及其线性组合1.1 向量
【定义1】n个有次序的数$a_{1}, a_{2}, \cdots, a_{n}$所组成的数组称为n维向量,这n个数称为该向量的n个分量,第i个数$a_i$称为第i个分量。
1.1.1 向量的表示法
n维向量写成一行,称为行向量,也称为行矩阵,常用$a^{T}, {b}^{T}, \alpha^{T}, \beta^{T}$等表示,如$a^{T}=\left(a_{1}, a_{2}, \cdots, a_{n}\right)$。
n维向量写成一列,称为列向量,也称为列矩阵,常用$a, {b}, \alpha, \beta$等表示。
说明:
行向量和列向量总看成两个不同的向量。
行向量和列向量都按矩阵的运算法则进行运算。
在没有明确说明时,向量均理解为列向量。
1.2 向量组与矩阵的关系由若干个同维数的列向量(或同维数的行向量)组成的集合,称为一个向量组。
反之,由有限个向量组成的向量组可以构成一个矩阵。
1.3 线性组合及线性表示
【定义2】给定向量组$A: a_{1}, a_{2}, \cdots, a_{m}$,对于任 ...
线性代数第3章:矩阵的初等变换与线性方程组
1 矩阵的初等变换1.1 矩阵的初等变换将解方程组的过程总结如下:
解方程组的方法称为消元法;
解方程组时,始终将方程看成一个整体变形,并且用到了如下三种变换
交换方程次序
以不为0的数乘某个方程
一个方程加上另一个方程的k倍
上述3种变换都是可逆的,由此变换前与变换后的方程组同解。
在上述变换过程中,只对方程组的系数和常数项进行运算,未知量并未参加运算,因此若记方程组的增广矩阵为:
则上述方程组的变换可转化为对矩阵B的变换。
1.1.1 定义1下列三种变换称为矩阵的初等行变换:
对换2行
以数$k \neq 0$乘某一行中的所有元素
某一行所有元素的k倍加到另一行对应元素上去
将定义中的“行”换成“列”,即得到矩阵的初等列变换的定义(所用记号是将“r”换成“c”)。
矩阵的初等行变换与初等列变换,统称为矩阵的初等变换。初等变换的逆变换也是初等变换,且与原变换的类型相同。
如果矩阵A经过有限次初等变换变成矩阵B,则称矩阵A与矩阵B等价,记作$A \sim B$。
矩阵之间的等价关系具有下列性质:
反身性:$A \sim A$
对称性:若$A \sim B$,则$B \s ...
6.23天津大学夏令营初筛机试
题目设置:一共5道题,只有10%~30%的样例。
考试时间:9:30~11:30,共2h。
1 题目A:整数化1.1 题目描述小Z在处理二维坐标点上的数据,受到性能限制,他希望把所有的点对应到距离它最近的整数点(横纵坐标均为整数)上, 请你帮他完成这个程序。
如果一个点有多个距离它最近的点,取横纵坐标更小的那个点。如(1, 1.5)将对应到(1, 1),(-1, -1.5)将对应到(-1, -2)。
1.2 输入多组样例输入,第一-行输入一个整数T表示样例数。
对于每个样例,包含两个数表示需要整型化的点。
1.3 输出对于每组样例,输出一行包含两个整数的坐标,用空格分割。
1.4 样例输入
31 1.52 3.2-1 -2
1.5 样例输出
1 12 3-1 -2
1.6 解题思路一开始直接使用了取整int(),但是当输入为负数的时候,例如-1.6取整为-1,但是题意要求是-2,所以应该判断一下小数部分和0.5的关系,分类讨论。
最终这个对于部分数据AC了,但是不知道剩下的数据怎么样。
12345678910111213141516171819202122232425262 ...
计网课设:基于TCP协议的简历聊天室程序设计
1 题目要求设计题目:基于TCP协议的简易聊天室程序设计
设计要求:使用Java编程语言,设计并实现一个基于TCP协议的简易聊天室程序。
程序包括服务器端和多个客户端,客户端能够连接到服务器并实现实时的聊天功能。
实现基本的用户登录、消息发送和接收功能。
2 整体架构设计在线聊天室程序通常采用客户端-服务器(C/S)架构设计如图3.1所示,其中服务器端负责管理用户连接、消息传递和群聊管理等核心功能,而客户端则提供用户界面,允许用户登录、发送消息和接收其他用户消息。
图3.1 TCP聊天室系统架构图
当设计一个聊天室程序时,除了客户端-服务器(C/S)架构外,通常还涉及到服务器与数据库的交互部分。服务器需要与数据库交互来存储用户的用户名和账号信息。
2.1 服务器端设计在日常生活中,服务器通常要同时接收来自客户端的多个请求,需要同时为这些客户端提供它们想要的服务,因此服务器端通常采用多线程或异步IO等技术,以支持多个客户端同时连接和消息处理。
在此次课程设计任务中,服务器实现的核心功能列举如下:
接受和管理连接:服务器通过绑定到特定端口的ServerSock ...
信息安全实验3:密码爆破
1 实验环境
操作系统版本:Windows 11 家庭中文版23H2
VMware® Workstation 16 Pro:16.2.3 build-19376536
Metasploitable2虚拟机版本:2.6.24-16-server
Kali虚拟机版本:6.6.9-amd64
2 实验内容Metasploitable2是一个特意设计用来进行渗透测试和漏洞分析的虚拟机。它基于Ubuntu Linux操作系统,包含了大量的已知漏洞,以便安全专业人员和研究人员可以使用渗透测试工具,如Metasploit等,来测试和验证其安全性。
Kali Linux是一种基于Debian Linux的渗透测试和网络安全分析的专用发行版。它旨在为安全专业人员、渗透测试人员和网络管理员提供一个功能强大的平台,用于评估系统和网络的安全性,并测试安全防御的有效性。Kali Linux包含了大量的渗透测试工具和网络安全工具,包括Metasploit框架、Nmap、Wireshark、Aircrack-ng等。这些工具涵盖了从信息收集、漏洞分析到渗透测试和数据包嗅探等多个方面,使用户能够全面地评估和测试目 ...
线性代数第2章:矩阵及其运算
1 线性方程组和矩阵1.1 线性方程组n个未知数m个方程的线性方程组如下:
上述线性方程组的解取决于系数a和常数项b。
当常数项b=0时,方程组
称为n元齐次线性方程组,当b≠0时,称为n元非齐次线性方程组。
线性方程组的系数和常数项按原位置可以排成数表如下:
对线性方程组的研究,可以转化为对此表的研究。
1.2 矩阵的定义由$m \times n$个数$a_{ij}(i=1,2,…,m;j=1,2,…,n)$排成的m行n列的数表
称为m行n列的矩阵,简称$m \times n$矩阵,记作
这$m \times n$个数称为矩阵A的元素,简称为元,数$a_{ij}$位于矩阵A的第i行第j列,$m \times n$矩阵A也可记作$A_{m \times n}$。
元素为实数的矩阵称为实矩阵;元素有虚数的矩阵称为复矩阵。
1.2.1 几种特殊的矩阵(1)行数和列数都等于n的矩阵称为n阶矩阵或n阶方阵,n阶矩阵A也记作$A_n$。
(2)只有一行的矩阵$A=\left(\begin{array}{llll}a_{1} & a_{2} ...
概率论第8章:假设检验
1 假设检验1.1 基本原理背景:在总体的分布函数完全未知或只知其形式、但不知其参数的情况下, 为了推断总体的某些性质,提出某些关于总体的假设。
例如, 提出总体服从泊松分布的假设;又如,对正态总体提出数学期望等于$\mu$的假设等.
假设检验就是根据得到的样本对所提出的假设作出判断: 是接受, 还是拒绝.
例1:某车间用一台包装机包装葡萄糖, 包得的袋装糖重是一个随机变量, 它服从正态分布.当机器正常时, 其均值为0.5千克, 标准差为0.015千克.某日开工后为检验包装机是否正常, 随机地抽取它所包装的糖9袋, 称得净重为(千克):0.497 0.506 0.518 0.524 0.498 0.511 0.520 0.515 0.512, 问机器这一天是否正常?
分析:用$\mu$和$\sigma$分别表示这一天袋装糖总体X的均值和标准差,由长期实践可知,标准差较稳定,设$\sigma=0.015$,则$X \sim N\left(\mu, 0.015^{2}\right)$,其中$\mu$未知。
目标:根据样本值判断$\mu&#x ...