信息安全实验4：文件上传
1 实验环境
操作系统版本：Windows 11 家庭中文版23H2
VMware® Workstation 16 Pro：16.2.3 build-19376536
Metasploitable2虚拟机版本：2.6.24-16-server
Kali虚拟机版本：6.6.9-amd64
2 实验内容编写木马程序文件muma.php，内容如下所示：
代码清单2.1 muma.php文件内容
1<?php @eval($_POST['176']) ?>
首先开启Metasploitable虚拟机，输入用户名和密码进行登录，之后输入“ifconfig”命令查看虚拟机的IP地址，如图2.1所示。
图2.1 查看`Metasploitable`虚拟机的IP地址
开启Kali虚拟机，在浏览器中输入上述IP地址访问Web服务，输入用户名和密码后进行登录，并设置网站的安全等级为“medium”，并点击“Submit”，操作内容如图2.2所示。
图2.2 设置网站安全等级
之后测试文件上传功能，点击“Upload”，选择木马程序文件muma.php文 ...
大佬演讲1：雷军2024年度演讲《勇气》
上了大学特别是学了计算机之后经常能够听到雷军的故事，他也是计算机专业，武汉大学毕业，所以更能感觉到共鸣吧。
之前也回看过雷军的演讲，但是今天有幸听了现场直播，感受如下。
1 遇到困难勇于面对
无论面对何等巨大的危机，都不能被吓到。破釜沉舟的勇气，才是冲出重围的关键。——雷军
小米造车源于一次来自美国的打击，之后雷总想，“如果哪一天小米不能造手机了，靠什么活下去？”，正是从此刻开始，小米有了造车的想法。
所以说，当遇到困难的时候，很多人想的是自己怎么这么难，生活不如意，为什么自己好倒霉等等。但是无论遇到什么困难，都应该有一个勇往直前的决心，正是困难才能让你不断进步，让你反思自己身上存在的问题，让你更加了解自己。
心态是一方面，同时也要采取行动去应对它，而不是等待困难自己消失。想想自己该怎么做，以及这么做是否对自己以及未来的自己是有益的？
2 尊重行业规律
守正出奇，要先守正再出奇，守正有时候比出奇更重要。——雷军
做什么行业，做什么事情要尊重行业或事情发展的规律，任何事物都有一个发展的过程，不能一蹴而就。小米造车，借鉴了其他车企成长的路线，当学习别人的方法的过程中，再逐渐产生自 ...
操作系统面经1：计算机系统概述
1 操作系统的目标和功能（什么是操作系统？）1.1 操作系统是计算机资源的管理者
处理机管理（进程控制、进程同步、进程通信、死锁处理、处理机调度）
存储器管理（提高内存利用率，内存的分配与回收、地址映射、内存保护与共享、内存扩充）
文件管理（计算机中的信息都是以文件的形式存在的）
设备管理（完成用户的I/O请求，方便用户使用设备、并提高设备的利用率）
1.2 操作系统为用户提供使用计算机硬件系统的接口
命令接口（用户通过控制台或终端输入操作命令，向系统提供各种服务要求）
程序接口（由 系统调用 组成，用户在程序中使用这些系统调用来请求操作系统为其提供服务）
图形接口 最常见的 图形用户界面GUI （最终还是通过调用程序接口实现的）
1.3 操作系统用作扩充机器没有任何软件支持的计算机称为裸机，实际呈现在用户面前的计算机系统是经过若干层软件改造的计算机。
操作系统将裸机改造成功能更强、使用更方便的机器。我们将覆盖了软件的机器称为扩充机器或虚拟机。
2 操作系统的运行机制？2.1 内核程序和应用程序(内核态和用户态)在计算机系统中，通常CPU执行两种不同性质的程序：一种是 ...
设计模式：单例
1 Intent确保一个类只有一个实例，并提供该实例的全局访问点。
2 Class Diagram使用一个私有构造函数、一个私有静态变量以及一个公有静态函数来实现。
私有构造函数保证了不能通过构造函数来创建对象实例，只能通过公有静态函数返回唯一的私有静态变量。
3 Implementation3.1 懒汉式-线程不安全以下实现中，私有静态变量 uniqueInstance被延迟实例化，这样做的好处是，如果没有用到该类，那么就不会实例化 uniqueInstance，从而节约资源。
这个实现在多线程环境下是不安全的，如果多个线程能够同时进入 if (uniqueInstance == null) ，并且此时 uniqueInstance为 null，那么会有多个线程执行 uniqueInstance = new Singleton(); 语句，这将导致实例化多次 uniqueInstance。
123456789101112public class Singleton { private static Singleton uniqueInstance; pri ...
第二期AI夏令营任务3：实现RAG应用
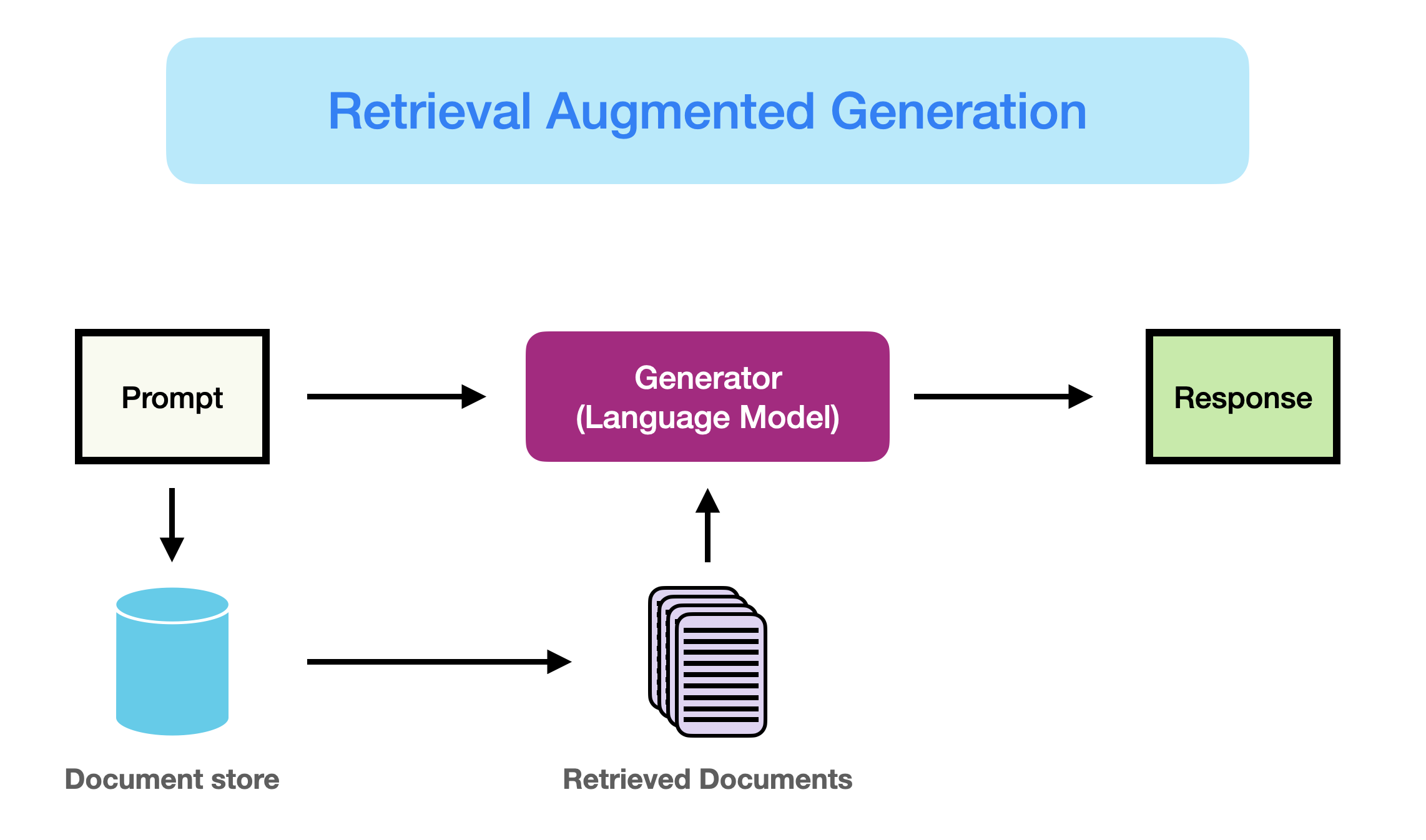
1 Gradio 技术入门Gradio是一个开源的 Python 库，用于快速构建机器学习和数据科学演示应用。它使得开发者可以在几行代码中创建一个简单、可调整的用户界面，用于展示机器学习模型或数据科学工作流程。Gradio支持多种输入输出组件，如文本、图片、视频、音频等，并且可以轻松地分享应用，包括在互联网上分享和在局域网内分享.
简单来说，利用 Gradio 库，我们可以很容易实现一个具有对话功能的前端页面，实现最简单人机交互功能。
在目前的深度学习软件开发中，使用gradio熟练展示demo已经成为了基础必备技能，你可以在任何地方（无论是学术还是工业界）见到 gradio 展示，但我们本次可以只从一个简单的对话demo开始，来逐渐展开gradio的熟悉之旅。
我们可以简单的理解为gradio就是在搭积木，或者说简单理解为所有的前端框架都是在利用一块块积木创造出最好的效果。
在gradio中，我们可以把每个组件创建在 gr.Blocks() 包裹的块当中，你可以把它当作一个展示台，我们可以在展示台上放满不同的组件（比如这里的 gr.Button，gr.Textbox 等等），你可 ...
天津大学智算夏令营之旅
1 夏令营安排
2 7月1日第一天刚起床的时候发现下雨了，但是自己并没有带伞，而且当时酒店里也没有伞，问了酒店客服，他说也没有。然后早上就穿着一个外套就出去了，幸亏这个外套是防雨的，外套外面都湿了，但是短袖一点没湿。
当时看到天津大学北洋园的第一印象是：这个学校好大啊，感觉比我本科的学校大了 10 多倍，而且这还只是一个校区。由于上午进行宣讲，而且还下着雨，就直接去教室了。
到了教室后，已经有很多的学生了，下面是当时拍的一个照片。
当时进到天大的一个教学楼，就感觉这个教学楼建的真好，感觉好大啊，而且教室里面的基础设施也很好，教室也真的好大，感觉天大好有钱。
之后就是每个团队的宣讲，主要感觉团队也很多，而且每个团队都有自己的体系，很有纪律。
记得上午的宣讲一直持续了很长时间，好像都快到下午 1 点了，当时挺饿的，宣讲结束之后就马上去吃饭了。天大中只有一个餐厅可以支持微信扫码，所以只能去那一个餐厅。
在去餐厅的路上，看到了天大的图书馆，如下图，是真的大，哭死/(ㄒoㄒ)/~~
到了餐厅，感觉它们餐厅真高级，直接扫桌子上的小程序进行点餐，也不用去前台点，但是感觉 ...
编译原理第6章：自底向上的语法分析
1 自底向上分析概述从分析树的底部(叶节点)向顶部(根节点)方向构造分析树，可以看成是将输入串w归约为文法开始符号S的过程。
自顶向下的语法分析采用最左推导方式
自底向上的语法分析采用最左归约方式（反向构造最右推导）
自底向上语法分析的通用框架：移入-归约分析(Shift-Reduce Parsing)。
1.1 移入-归约分析的工作过程在对输入串的一次从左到右扫描过程中，语法分析器将零个或多个输入符号移入到栈的顶端，直到它可以对栈顶的一个文法符号串β进行归约为止。
然后，它将β归约为某个产生式的左部，语法分析器不断地重复这个循环，直到它检测到一个语法错误，或者栈中包含了开始符号且输入缓冲区为空(当出现这种情况时，语法分析器停止运行，并宣称成功完成了语法分析)为止。
1.2 移入-归约分析器可采取的4种动作
移入：将下一个输入符号移到栈的顶端
归约：被归约的符号串的右端必然处于栈顶。语法分析器在栈中确定这个串的左端，并决定用哪个非终结符来替换这个串
接收：宣布语法分析过程成功完成
报错：发现一个语法错误，并调用错误恢复子例程
移入-归约分析中存在的问题：如何正确地识别句柄？
...
编译原理第4章：自顶向下的语法分析
1 自顶向下分析概述
从分析树的顶部（根节点）向底部（叶节点）方向构造分析树，可以看成是从文法开始符号$S$推导出词串$w$的过程。
每一步推导中，都需要做两个选择：
替换当前句型中的哪个非终结符
用该非终结符的哪个候选式进行替换
1.1 最左推导在最左推导中，总是选择每个句型的最左非终结符进行替换。
如果$\boldsymbol{S} \Rightarrow{ }_{l m}^{*} \boldsymbol{\alpha}$，则称$\alpha$是当前文法的最左句型（left-sentential form）。
1.2 最右推导在最右推导中，总是选择每个句型的最右非终结符进行替换。
在自底向上的分析中，总是采用最左归约的方式，因此把最左归约称为规范归约，而最右推导相应地称为规范推导。
1.3 最左推导和最右推导的唯一性
如果最左推导和最右推导生成的语法树不是唯一的，那么这个文法就有二义性。
1.3.1 自顶向下的语法分析采用最左推导方式
总是选择每个句型的最左非终结符进行替换
根据输入流中的下一个终结符，选择最左非终结符的一个候选式
1.4 自顶向下语法分析的通用形式1 ...
编译原理第3章：词法分析
1 词法分析程序的设计1.1 词法分析流程逐个读入源程序字符并按照构词规则切分成一系列单词（token）。
单词是语言中具有独立意义的最小单位，包括保留关键字、标识符、常量、运算符、标点符号、分界符等。
词法分析是编译过程中的一个阶段，在语法分析前进行，也可和语法分析结合在一起作为一遍，由语法分析程序调用词法分析程序来获得当前单词供语法分析使用。
词法分析程序的主要任务及输出：
读源程序，产生用二元组表示的单词符号
滤掉空格，跳过注释、换行符
记录源程序的行号，以便出错处理程序准确定位源程序的错误
宏展开等…
2 正则表达式
正则表达式（Regular Expression，RE）是一种用来描述正则语言的更紧凑的表示方法。
例如：$r = a (a \mid b)^* (\varepsilon \mid(. \mid \_ )(a \mid b)(a \mid b)^*)$
正则表达式可以由较小的正则表达式按照特定规则递归地构建。每个正则表达式 $r$ 定义（表示）一个语言，记为$L(r)$。
这个语言也是根据 $r$ 的子表达式所表示的语言递归定义的。
2.1 ...
线性代数第4章：向量组的线性相关性
1 向量组及其线性组合1.1 向量
【定义1】n个有次序的数$a_{1}, a_{2}, \cdots, a_{n}$所组成的数组称为n维向量，这n个数称为该向量的n个分量，第i个数$a_i$称为第i个分量。
1.1.1 向量的表示法
n维向量写成一行，称为行向量，也称为行矩阵，常用$a^{T}, {b}^{T}, \alpha^{T}, \beta^{T}$等表示，如$a^{T}=\left(a_{1}, a_{2}, \cdots, a_{n}\right)$。
n维向量写成一列，称为列向量，也称为列矩阵，常用$a, {b}, \alpha, \beta$等表示。
说明：
行向量和列向量总看成两个不同的向量。
行向量和列向量都按矩阵的运算法则进行运算。
在没有明确说明时，向量均理解为列向量。
1.2 向量组与矩阵的关系由若干个同维数的列向量（或同维数的行向量）组成的集合，称为一个向量组。
反之，由有限个向量组成的向量组可以构成一个矩阵。
1.3 线性组合及线性表示
【定义2】给定向量组$A: a_{1}, a_{2}, \cdots, a_{m}$，对于任 ...
