面试记录6:快手技术一面
1 面试背景
- 面试公司:快手
- 面试岗位:推荐算法实习生【模型算法】
- 面试类型:技术一面
- 面试时间:2024-12-06 15:00~16:00
- 面试结果:通过 😊
2 整体感受
在面试之前就很想去快手,所以很期待这次面试。面试官一进来感觉挺和善的,而且他还简单自我介绍了一下。面试官看起来年龄不是很大,感觉接近 30 的样子。
在面试过程中面试官会引导你去思考,有的问题并不是想问出来一个确切的答案,就是想让你自己去思考一下。所以我就遇到了很多开放的题目。
后面有两道手撕代码,第一道算笛卡尔积,第二道是动态规划,几乎都做出来了。整体感受还不错吧,但是还是要等面试结果出来。
3 提问的问题
3.1 word2Vec
面试官:我看你这里用了一个 w2v 的方式对吧,能介绍一下基本的原理吗?
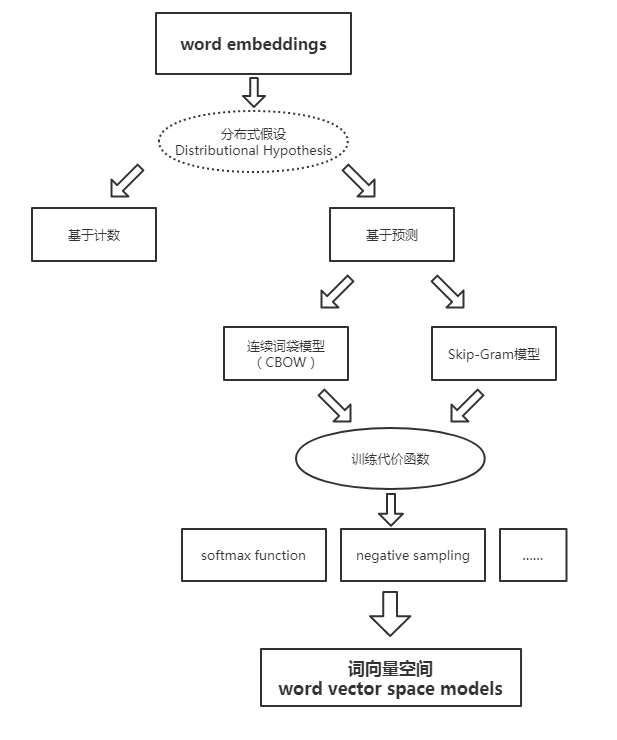
首先介绍一下 Word2Vec,Word2Vec 是一个生成对“词”的向量表达的模型。分为词袋模型和跳元模型。
利用物品序列是由特定用户的浏览、购买等行为产生的历史行为记录序列来生成 Embedding。输入向量表达就是输入层到隐层的权重矩阵 $\mathcal{W}_{V \times N}$,而输出向量表达就是隐层到输出层的权重矩阵 $\mathcal{W}^{‘}_{N \times V}$。
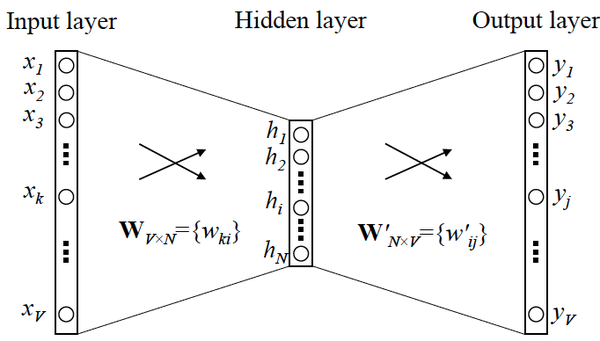
在获得输入向量矩阵 $\mathcal{W}_{V \times N}$ 后,其中每一行对应的权重向量就是通常意义上的“词向量”。于是这个权重矩阵自然转换成了 Word2Vec 的查找表(lookup table)。
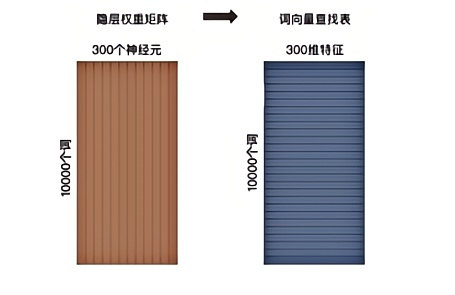
假设语料库中的词的数量为 10000,就意味着输出层神经元有 10000 个,在每次迭代更新隐层到输出层神经元的权重时,都需要计算所有字典中的所有 10000 个词的预测误差(prediction error),在实际训练过程中几乎无法承受这样巨大的计算量。
为了减轻 Word2Vec 的训练负担,往往采用负采样(Negative Sampling)的方法进行训练。相比原来需要计算所有字典中所有词的预测误差,负采样方法只需要对采样出的几个负样本计算预测误差。
在此情况下, Word2Vec 模型的优化目标从一个多分类问题退化成了一个近似二分类问题,如下式所示:
$$
E=-\log \sigma\left(\boldsymbol{v}_{w_{o}}^{\prime}{ }^{\mathrm{T}} \boldsymbol{h}\right)-\sum_{w_{j} \in W_{\text {neg }}} \log \sigma\left(-\boldsymbol{v}_{w_{j}}^{\prime}{ }^{\mathrm{T}} \boldsymbol{h}\right)
$$
其中 $\boldsymbol{v}_{w_{o}}^{\prime}$ 是输出词向量(即正样本),$\boldsymbol{h}$ 是隐层向量,$W_{neg}$ 是负样本集合,$\boldsymbol{v}_{w_{j}}^{\prime}$ 是负样本词向量。一般来说负样本集合的规模 $k$ 在小数据集中取 2~5,在大数据集中取 5~20,所以计算量会大大降低。
实际上,加快 Word2Vec 训练速度的方法还有分层 softmax,但实现较为复杂,且最终效果没有明显由于负采样方法,因此较少采用。
3.1.1 分层 softmax
面试官:你刚才也说到 w2v 有两种方式,你知道比如他做层次 softmax 的时候,在梯度更新的时候,它是由叶子节点和非叶子结点,这一块你知道是怎么去分析的吗?
层序 softmax(hierarchical softmax)使用二叉树,其中树的每个叶节点表示词表 $\mathcal{V}$ 中的一个词。
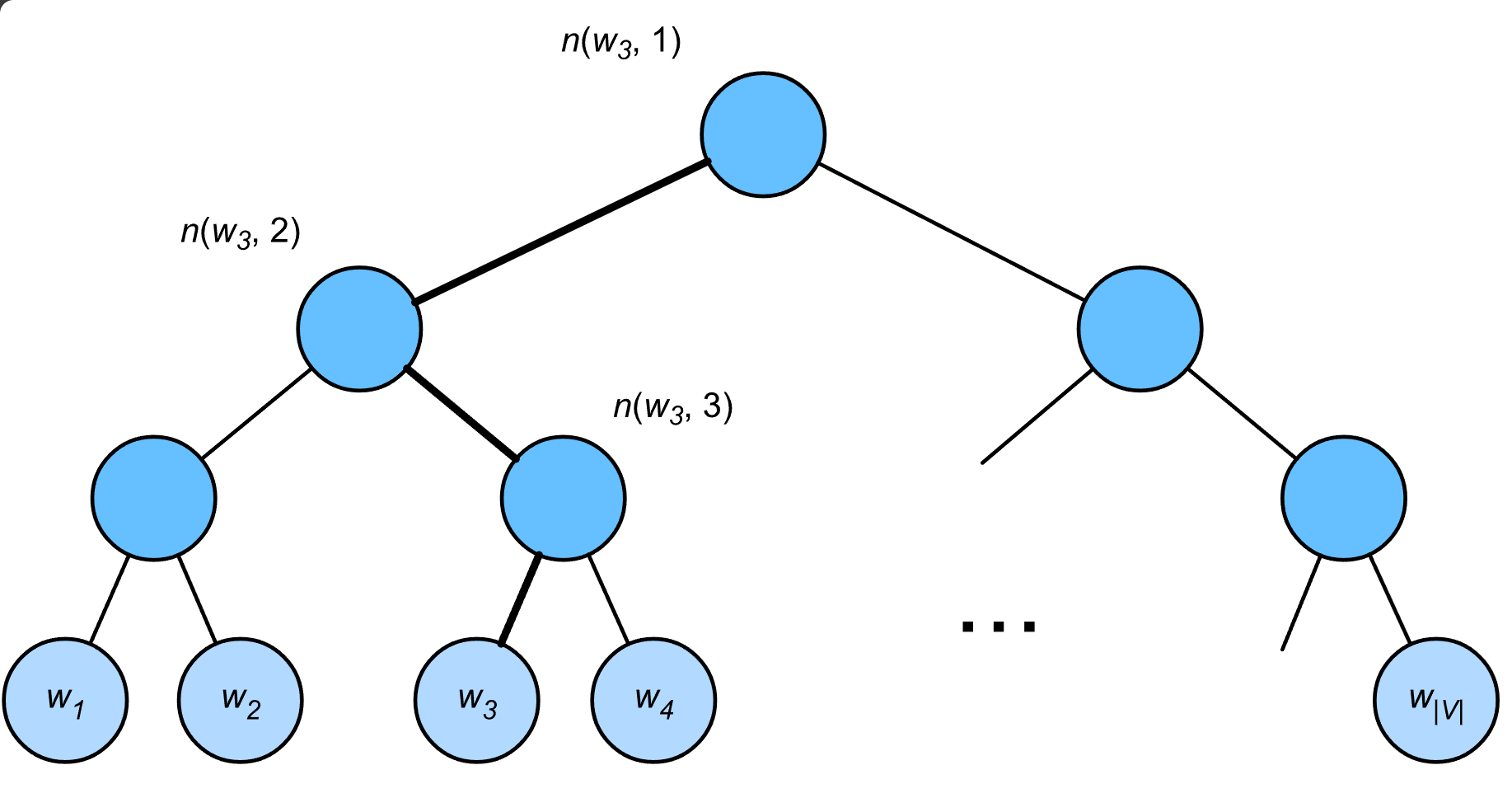
用 $L(w)$ 表示二叉树中表示字 $w$ 的从根节点到叶节点的路径上的节点数(包括两端)。设 $n(w,j)$ 为该路径上的 $j^\mathrm{th}$ 节点,其上下文字向量为 $\mathbf{u}_{n(w, j)}$。例如,$L(w_3) = 4$。分层softmax将 条件概率近似为:
$$
P(w_o \mid w_c) = \prod_{j=1}^{L(w_o)-1} \sigma\left( [![ n(w_o, j+1) = \text{leftChild}(n(w_o, j)) ]!] \cdot \mathbf{u}_{n(w_o, j)}^\top \mathbf{v}_c\right)
$$
其中函数 $\sigma$ 为 sigmoid 激活函数,$\text{leftChild}(n)$ 是节点 $n$ 的左子节点:
- 如果 $x$ 为真,$[[x]] = 1$
- 否则 $[[x]] = -1$
为了说明,让我们计算给定词 $w_c$ 生成词 $w_3$ 的条件概率。这需要 $w_c$ 的词向量 $\mathbf{v}_c$ 和从根到 $w_3$ 的路径(上图中加粗的路径)上的非叶节点向量之间的点积,该路径依次向左、向右和向左遍历:
$$
P(w_3 \mid w_c) = \sigma(\mathbf{u}_{n(w_3, 1)}^\top \mathbf{v}_c) \cdot \sigma(-\mathbf{u}_{n(w_3, 2)}^\top \mathbf{v}_c) \cdot \sigma(\mathbf{u}_{n(w_3, 3)}^\top \mathbf{v}_c)
$$
由 $\sigma(x)+\sigma(-x) = 1$,它认为基于任意词 $w_c$ 生成词表 $\mathcal{V}$ 中所有词的条件概率总和为 $1$:
$$
\sum_{w \in \mathcal{V}} P(w \mid w_c) = 1
$$
幸运的是,由于二叉树结构,$L(w_o)-1$ 大约与 $\mathcal{O}(\text{log}_2|\mathcal{V}|)$ 是一个数量级。当词表大小 $\mathcal{V}$ 很大时,与没有近似训练的相比,使用分层 softmax 的每个训练步的计算代价显著降低。
3.1.2 负采样
面试官:降采样的话你知道是怎么做的吗?
负采样修改了原目标函数。给定中心词 $w_c$ 的上下文窗口,任意上下文词 $w_o$ 来自该上下文窗口的被认为是由下式建模概率的事件:
$$
P(D=1\mid w_c, w_o) = \sigma(\mathbf{u}_o^\top \mathbf{v}_c)
$$
其中 $\sigma$ 使用了 sigmoid 激活函数的定义:
$$
\sigma(x) = \frac{1}{1+\exp(-x)}
$$
从最大化文本序列中所有这些事件的联合概率开始训练词嵌入。具体而言,给定长度为 $T$ 的文本序列,以 $w^{(t)}$ 表示时间步 $t$ 的词,并使上下文窗口为 $m$,考虑最大化联合概率:
$$
\prod_{t=1}^{T} \prod_{-m \leq j \leq m,\ j \neq 0} P(D=1\mid w^{(t)}, w^{(t+j)})
$$
然而,上式只考虑那些正样本的事件。仅当所有词向量都等于无穷大时,上式中的联合概率才最大化为1。当然,这样的结果毫无意义。为了使目标函数更有意义,负采样添加从预定义分布中采样的负样本。
用 $S$ 表示上下文词 $w_o$ 来自中心词 $w_c$ 的上下文窗口的事件。对于这个涉及 $w_o$ 的事件,从预定义分布 $P(w)$ 中采样 $K$ 个不是来自这个上下文窗口噪声词。用 $N_k$ 表示噪声词 $w_k$($k=1, \ldots, K$)不是来自 $w_c$ 的上下文窗口的事件。假设正例和负例 $S, N_1, \ldots, N_K$ 的这些事件是相互独立的。负采样将上式中的联合概率(仅涉及正例)重写为:
$$
\prod_{t=1}^{T} \prod_{-m \leq j \leq m,\ j \neq 0} P(w^{(t+j)} \mid w^{(t)})
$$
通过事件 $S, N_1, \ldots, N_K$ 近似条件概率:
$$
P(w^{(t+j)} \mid w^{(t)}) =P(D=1\mid w^{(t)}, w^{(t+j)})\prod_{k=1,\ w_k \sim P(w)}^K P(D=0\mid w^{(t)}, w_k)
$$
分别用 $i_t$ 和 $h_k$ 表示词 $w^{(t)}$ 和噪声词 $w_k$ 在文本序列的时间步 $t$ 处的索引。上式中关于条件概率的对数损失为:
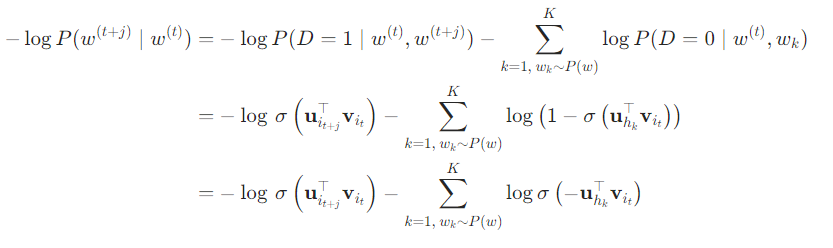
我们可以看到,现在每个训练步的梯度计算成本与词表大小无关,而是线性依赖于 $K$。当将超参数 $K$ 设置为较小的值时,在负采样的每个训练步处的梯度的计算成本较小。


3.1.3 高频词和低频词
对于低频词,会设置阈值(默认 $5$),对于出现频次低于该阈值的词会直接舍弃,同时训练集中也会被删除。
高频词提供的信息相对较少,为了提高低频词的词向量质量,有必要对高频词进行限制。高频词对应的词向量在训练时,不会发生明显的变化,因此在训练是可以减少对这些词的训练,从而提升速度。
源码中使用 Sub-Sampling 技巧来解决高频词的问题,能带来 2~10 倍的训练速度提升,同时提高低频词的词向量精度。
给定一个词频阈值 $t$ ,将 $w$ 以 $p(w)$ 的概率舍弃,$p(w)$ 的计算如下:
$$
\begin{aligned} p(w) & =1-\sqrt{\frac{t}{\operatorname{len}(w)}} \ \text { where } \operatorname{len}(w) =\frac{\operatorname{count}(w)}{\sum_{u \in V} \operatorname{count}(u)}\end{aligned}
$$
3.2 推荐系统中的特征工程
面试官:你知道常见的推荐系统里面的特征分成哪几类?
可以分成用户特征、物品特征和用户物品交互特征。
面试官:比如这三类特征下面,你感觉比如这几类哪一类特征你觉得是更重要一些的?
用户行为数据(User Behavior Data)是推荐系统最常用,也是最关键的数据。用户的潜在兴趣、用户对物品的真实评价都包含在用户的行为历史中。
用户行为在推荐系统中一般分为显性反馈行为(Explicit Feedback)和隐性反馈行为(Implicit Feedback)两种,在不同的业务场景中,它们会以不同的形式体现,如下图所示:

对用户行为数据的使用往往涉及对业务的理解,不同的行为在抽取特征时的权重不同,而且一些跟业务特点强相关的用户行为需要推荐工程师通过自己的观察才能发现。
在当前的推荐系统特征工程中,隐性反馈行为越来越重要,主要原因是显性反馈行为的收集难度过大,数据量小。在深度学习模型对数据量的要求越来越大的背景下,仅用显性反馈的数据不足以支持推荐系统训练过程的最终收敛。所以,能够反映用户行为特点的隐性反馈是目前特征挖掘的重点。
3.3 SIM 模型
面试官:你知道 DIN 模型之后,一系列的序列建模的模型的思路是怎么样的,比如 SIM2.0、SIM3.0之类的?
详见:https://juejin.cn/post/7263730927087452219
3.4 特征交叉
面试官:特征交叉可以想一下,在进入模型之后,因为所有的特征都会变成一个向量,然后做特征交叉的时候,可以分成这么几类,比如说在单个特征上有一个 $8$ 维的向量,每一维里面的向量其实也是可以做一些交叉的,称之为 bit-wise 的一个交叉,这种有了解过吗?可以往注意力机制那块去想一想。
在推荐系统中,特征交叉是一种常用的手段,可以捕捉特征之间的相互作用,提升模型性能。特征交叉分为bit-wise、element-wise、和vector-wise三种方式。
bit-wise:逐位进行特征交叉,通常适用于二进制特征;
在进行交互时,交互的形式类似于 $f(w_1 \times (a_1 \times a_2), w_2 \times (b_1 \times b_2), w_3 \times (c_1 \times c_2))$,此时认为特征交互是发生在元素级(bit-wise)上。
element-wise:逐元素进行特征交叉,适合连续特征或高维特征;
vector-wise:通过向量级别的交叉,可以捕捉更复杂的特征关系。
如果特征交互形式类似于 $f(w \times (a_1 \times a_2 ,b_1 \times b_2,c_1 \times c_2))$,那么我们认为特征交互是发生在特征向量级(vector-wise)。
3.5 多任务推荐算法
面试官:你对多目标多任务这一块有什么了解吗?
3.5.1 ESMM
ESMM 在多任务学习中比较特殊,因为其优化的两个目标 — CTR 和 CVR,是有着严格的先后顺序的(转化行为必然发生在点击之后)。也正因如此,ESMM 的通用性不强,但由于其瞄准的两个目标在推荐系统中是最重要的,因此这个算法的影响还是很大的。
ESMM 主要想解决的两个问题分别是样本选择偏差(SSB,sample selection bias)以及数据稀疏(DS,data sparsity)。SSB 其实就是在训练 CVR 模型时由于只对点击样本进行训练而产生的训练和线上样本的分布偏差。用户完整的行为链路是 曝光 → 点击 → 转化 ,离线训练的样本抽取的是点击样本,而线上预测时面对的则是曝光样本,那这中间肯定会有一个 gap。DS 则比较好理解,就是点击样本比较少,转化行为更加稀疏。
第一个问题则确实是一个“痛点”。作者给出的方法是对 CTR 和 CTCVR(而不是 CVR)进行联合建模, CVR 通过 CTCVR/CTR 间接得到。这样做的好处是可以利用所有曝光样本对两个目标进行训练,来解决 SSB 的问题;同时通过共享 embedding 层来解决 DS 问题。整个模型的结构类似于双塔,CVR 和 CTR 通过相乘连接得到 CTCVR。
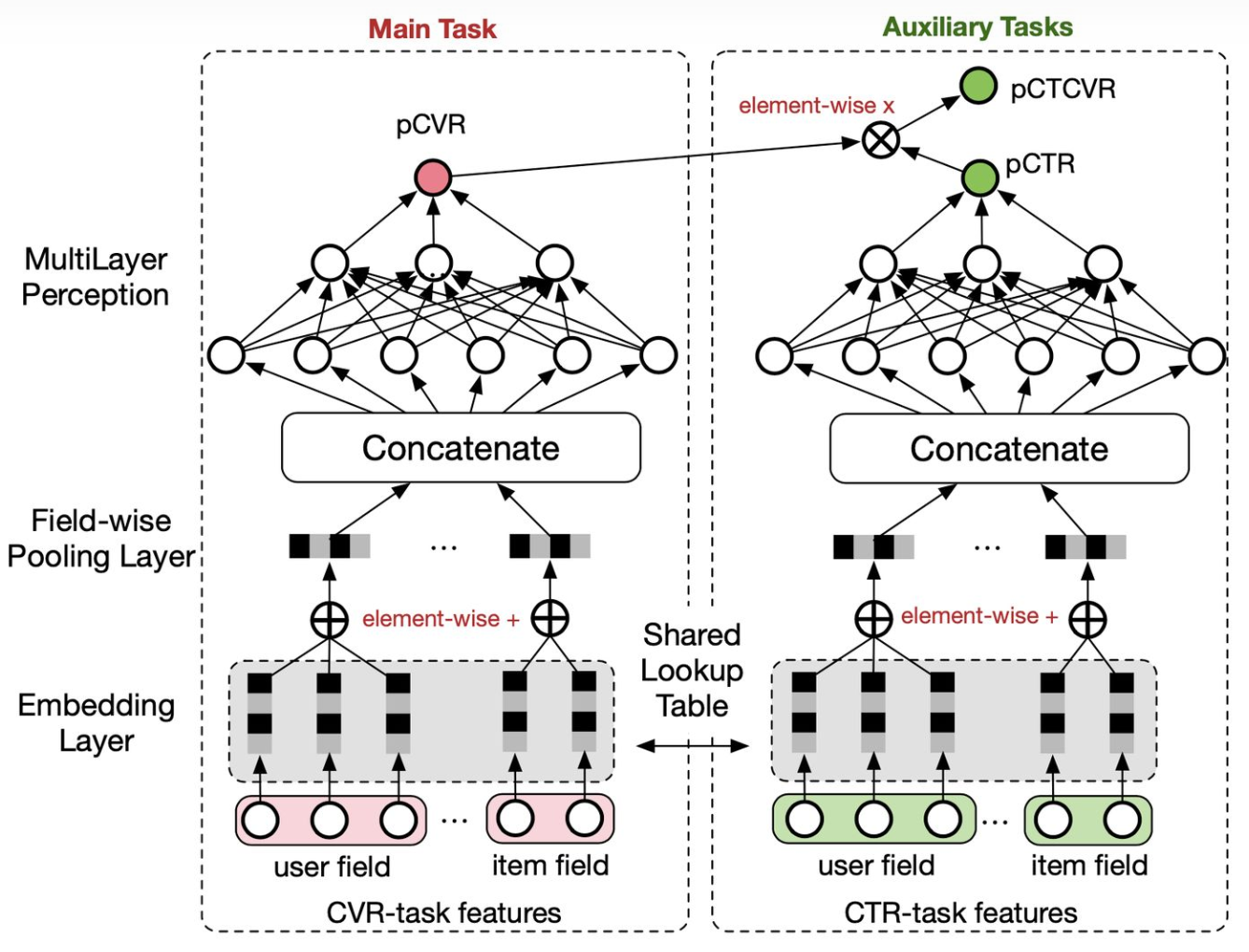
这个方法主要还是为了解决 CVR 预估上的问题,对于 CTR 任务来说效果可能一般,两个任务的效果容易出现跷跷板现象(即此消彼长)。
3.5.2 MMoE
MMoE 由底层共享(Shared-Bottom)演变而来。底层共享模型结构如下图 a 所示,其实就是多任务之间共享底层网络:
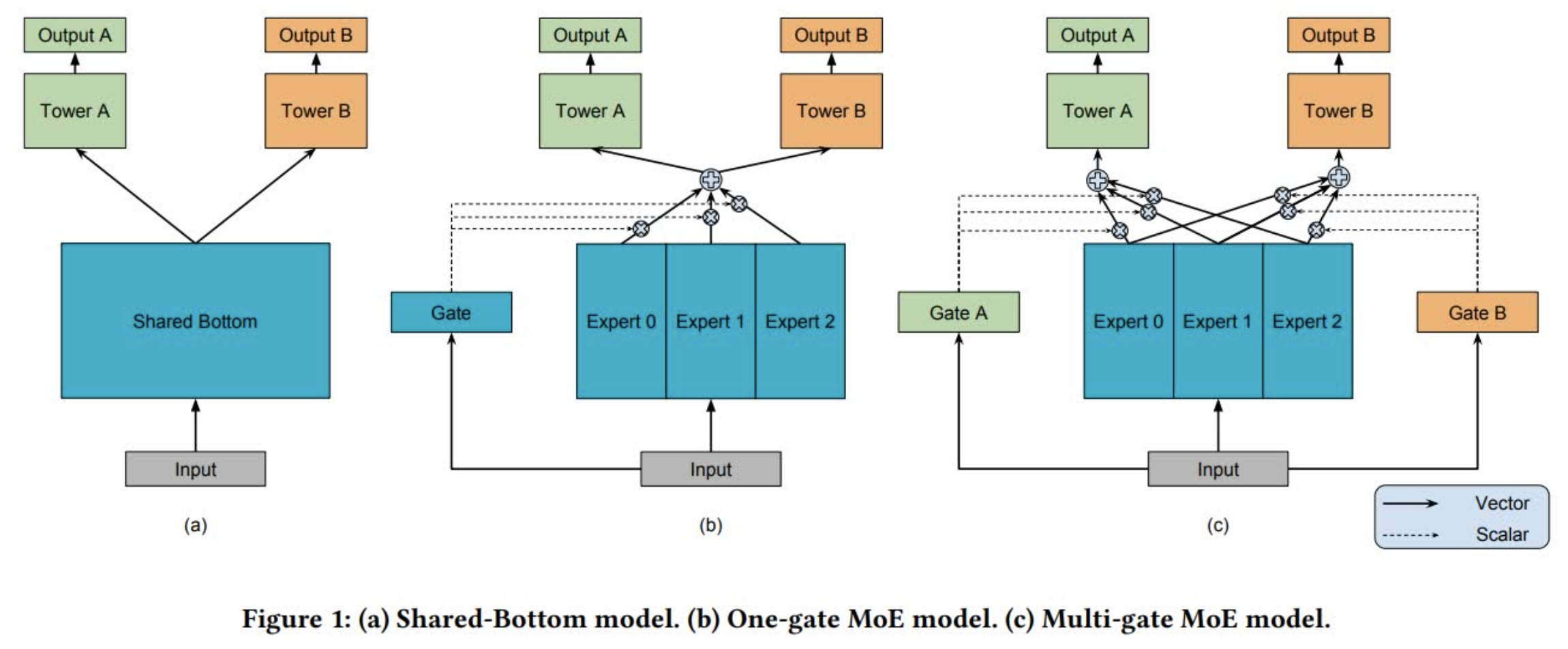
MoE(Mixture-of-Experts)基于底层共享进行了改进,将共享网络拆分成多个并行的子网络(即专家网络),并通过 Gate 进行各个专家网络的权重调节。这里对于各个任务,底层的网络仍然是一样的,不同任务都会对 Gate 和专家网络产生影响,因此可以理解为是多个底层网络的集成,集成权重由网络输入(即样本)自适应调节。当各个任务训练样本重合度比较小时,Gate 或许也可以理解为一种和任务相关的对底层网络的集成控制,但是当重合度比较高时,这个区别或许就不明显了。此外,采用这种结构的好处是可以通过给 Gate 引入稀疏性而降低训练和测试时的计算量,带来性能提升。
MMoE(Multi-gate Mixture-of-Experts)在 MoE 的基础上引入多个 Gate,每个任务都有一个独立的 Gate,相当于每个任务都可以训练出一个和自身任务更匹配的专家网络加权网络。当各个任务之间的关联度比较小的时候,MMoE 通过引入更多参数(即多个 Gate)可以学习到对于不同任务来说更好的专家网络集成方式,通常也会比 MoE 取得更好的效果。此外,由于单个 Gate 的参数量比较少,因此即便是引入多个 Gate,总体的参数量和 MoE 还是接近的,性能上的收益还是有的。
这篇发表在 RecSys2019 上的文章描绘了 MMoE 是如何在 Youtube 视频推荐场景上应用的。这里的场景设定简单来说就是给用户推荐下一个他/她可能感兴趣并且愿意观看的视频,候选集是粗排后的几百个视频,这里要做的是进行进一步地精排。目标有两种,一种是参与目标(engagement objective),例如点击和观看;另一种是满意度目标(satisfaction objective),例如点赞和屏蔽。针对不同目标就可以采用 MMoE 构建不同的 Gate 网络进行控制,整个网络架构如下图所示:
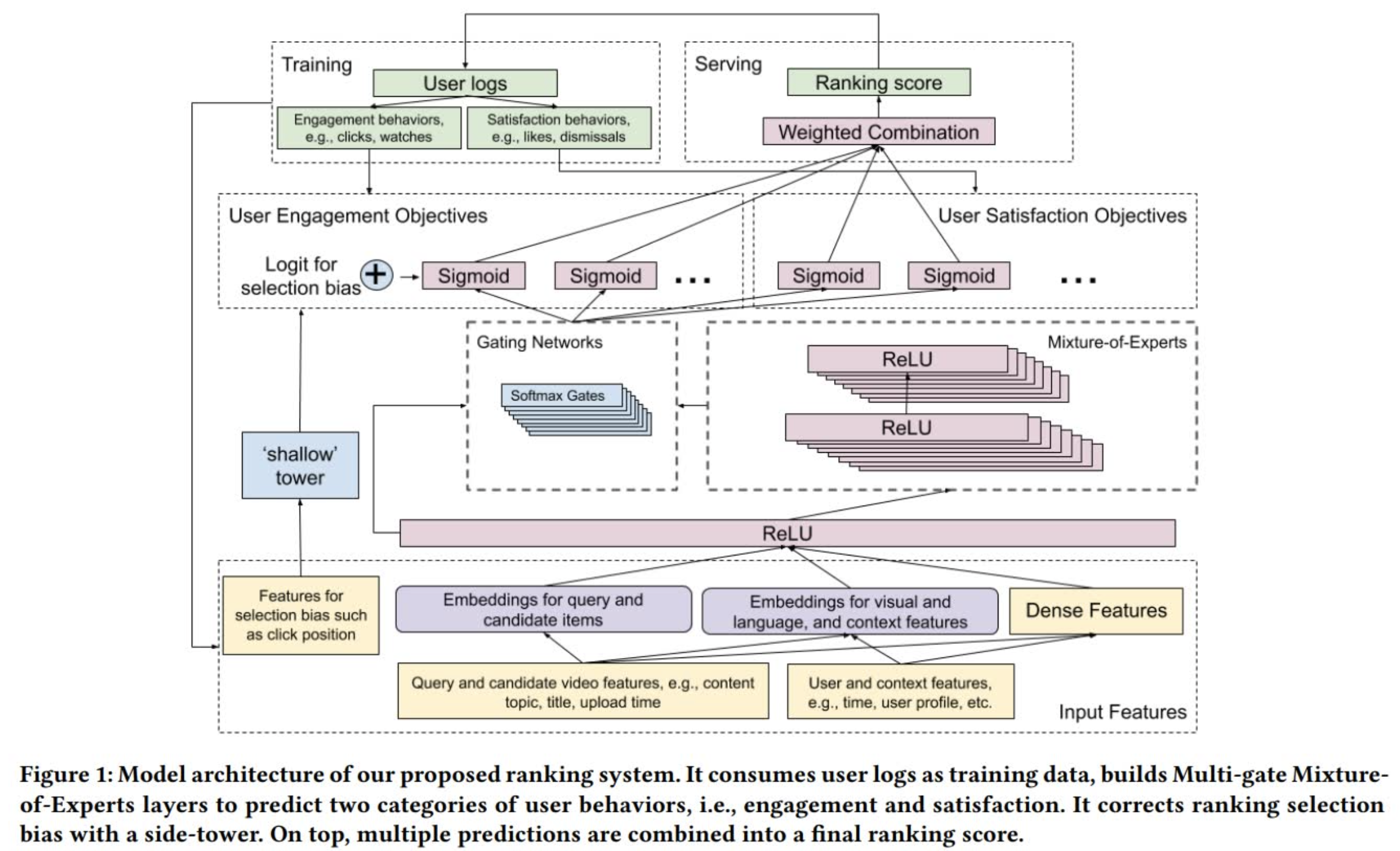
这里有一个细节比较有意思,就是在 MoE 层之前,输入层之后还有一层全连接层,它的作用主要是用来减少计算量。因为输入层的维度往往非常大,如果直接连接 MoE,那么有 $n$ 个任务,参数就翻 $n$ 倍,但是一旦接入一层全连接层(即 Shared Bottom Layer),那么参数会少很多。
3.5.3 SNR
SNR 全称是子网络路由(Sub-Network Routing),顾名思义就是提供一种对于每个任务来说更灵活的子网络联通方式。它和 MMoE 一样都是从 Shared Bottom 结构演变而来,相比于 MMoE 中各自独立的多个专家网络,SNR 提供了一种更灵活的子网络切分和联通的方式(本质上也就是参数共享方式):
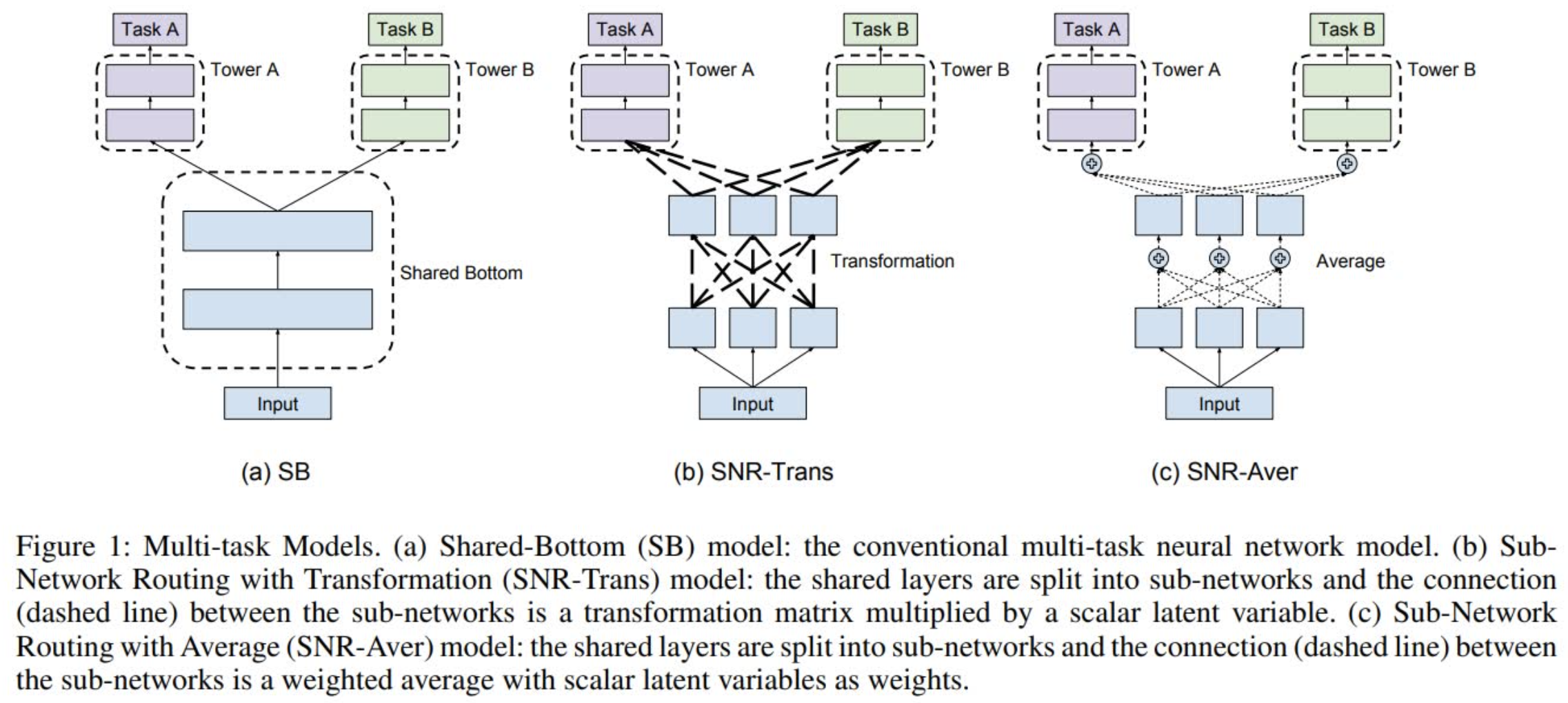
正如上图所示,SNR 分成 SNR-Trans 和 SNR-Aver 两种。对于 SNR-Trans,上下两层的子网络通过线性变换连接,而 SNR-Aver 则是直接加权平均。两个子网络之间是否联通由编码变量(Coding Variable)$z$ 决定,$z=1$ 表示连通,$z=0$ 则表示不连通。假设有两层相邻网络,其中 $u_1,u_2,u_3$ 分别表示低一层子网络的输出,而 $v_1,v_2$ 则表示高一层子网络的输入,那么 SNR-Trans 可以被表示为:
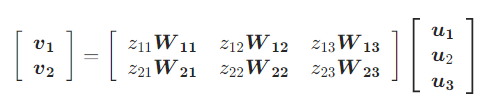
其中 $W_{ij}$ 是从第 $j$ 个低层子网络向第 $i$ 个高层子网络的变换矩阵。而 SNR-Aver 则是:
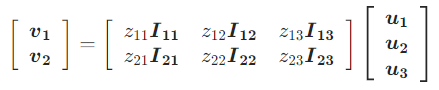
其中 $I_{ij}$ 就是单位矩阵。假设我们有两个相同参数个数的 SNR-Trans 和 SNR-Aver 模型,那么 SNR-Trans 模型就会在层连接上有更多参数,而 SNR-Aver 模型则是在子网络内有更多参数。也正因为如此, SNR-Trans 网络更容易进行参数裁剪,因为只要某两个子网络不连接,就没必要有对应的变换矩阵;但是对于 SNR-Aver 网络来说,则必须某个子网络和所有其他子网络都不连接,才能被裁剪掉。
4 手撕代码
4.1 DFS
给你三个数组:$[1, 2], [3, 4], [5, 6]$,计算得到它们的笛卡尔积为:
$$
[1, 3, 5], [1, 3, 6], [1, 4, 5], [1, 4, 6], [2, 3, 5], [2, 3, 6], [2, 4, 5], [2, 4, 6]
$$
当时看到这道题我其实忘记了笛卡尔积是什么,感觉这方面有些薄弱,因此总结在 4.3 节。
一开始我说直接用三重循环,枚举每一种可能,但是面试官时间复杂度太高了,让我再想一下其他做法。然后我就一直想能进行什么优化呢?一点想不出来。然后面试官问我了解过 DFS 和 BFS 吗?我说我知道,然后就提示我用 DFS 做。
我当时就很纳闷,用 DFS 能进行什么优化?不还是要遍历每一种组合吗?但是当时并没有想太多,就赶紧按照面试官给我的提示开始写 DFS 了。
1 | ans = [] |
当时写完了之后运行是不对的,面试官一直提示我是不是没有保存遍历过的状态,是不是应该用一个数据结构来保存一下,我当时没有听,因为我感觉不是那个问题。
原因是第一遍写的时候没有写成 t = path.copy() ,而是写成了 t = path ,就是这个问题。在 Python 里这么写 t 是 path 的一个引用,在改变 t 的时候,path 也会被改变,所以肯定不对鸭!!!
也可以改成下面这种写法:
1 | def dfs(i, path): |
还有其他几种方法可以在深度优先搜索(DFS)中避免修改同一对象:
- 使用切片:
t = path[:] - 使用
list()函数:t = list(path)
DFS 一共遍历过 $2 \times 2 \times 2$ 个状态,所以时间复杂度为 $O(n^3)$,其中 $n=2$ 。但是,如果我用以下三重循环,时间复杂度不也是 $O(n^3)$ 吗?
1 | for i in range(2): |
所以感觉面试官有点离谱……
4.2 动态规划
第二道是一个动态规划,给你一个数组 $[3, 1, 7, 10]$ ,求其中不连续子数组的和的最大值,同时要输出这个最大和的子数组。该题中 $[3, 7],[3, 10], [3, 10], [1, 10]$ 是所有不连续的数组,最大的和是 $13$,那么输出 $[3, 10]$。
可以用动态规划来做,如下:
- 状态表示:
- $f[i]$ 表示以第 $i$ 个元素结尾的不连续子数组的最大和
- $states[i]$ 表示以第 $i$ 个元素结尾的不连续子数组
- 状态计算:
$$
f[i] = \max(f[i], f[j] + \text{nums}[i]),j\in [0, i - 2]
$$
代码实现如下:
1 | nums = [3, 1, 10, 5] |
第一遍写完了之后还是出现问题,面试官一直提示我说双循环里面是不是没有考虑 else 代码块需要进行的操作,后来发现还是 copy() 的问题,只能说面试官是好心的。
4.3 向量各种乘积
4.3.1 笛卡尔积
笛卡尔积是指在数学中,两个集合 $X$ 和 $Y$ 的笛卡尓积(Cartesian Product),又称直积,表示为 $X \times Y$,第一个对象是 $X$ 的成员而第二个对象是 $Y$ 的所有可能有序对的其中一个成员。
假设有 $A=\{a,b\}, B=\{0,1,2\}$,则:
$$
A×B=\{(a, 0), (a, 1), (a, 2), (b, 0), (b, 1), (b, 2)\}
$$
$$
B×A=\{(0, a), (0, b), (1, a), (1, b), (2, a), (2, b)\}
$$
4.3.2 哈达玛积
哈达玛积又叫做按元素乘法。

4.3.3 矩阵内积
矩阵内积就是两个大小相同的矩阵元素一一对应相乘并且相加。

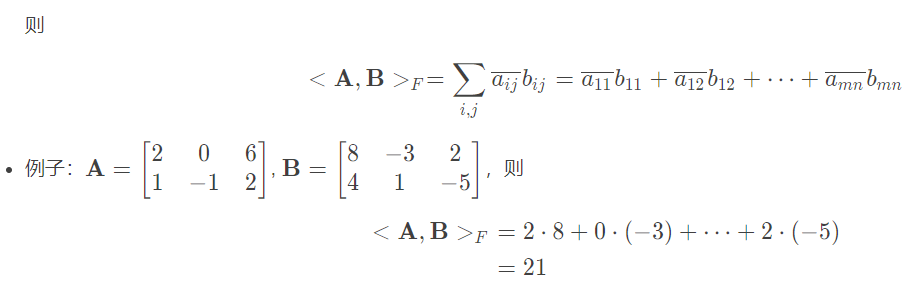
4.3.4 点积(内积)
矩阵内积退化成向量形式就是点积,也可以称作向量内积。两个向量里元素一一相乘,再相加。
适用范围:维度相同的两个向量。
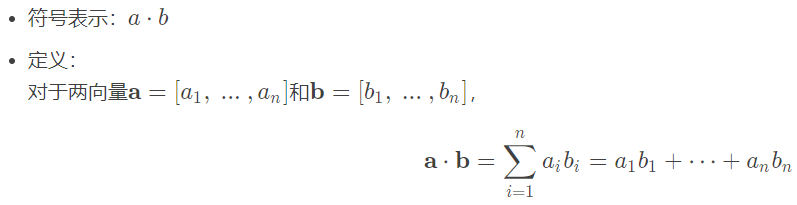
4.3.5 外积
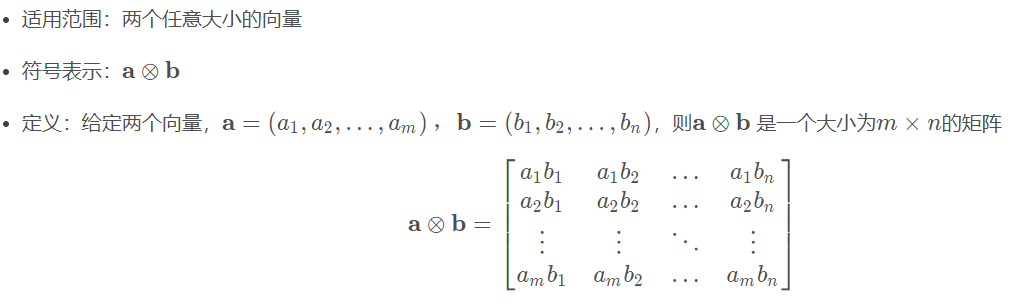
4.3.6 克罗内克积










