1 线性方程组和矩阵

1.1 线性方程组

n个未知数m个方程的线性方程组如下：

上述线性方程组的解取决于系数a和常数项b。

当常数项b=0时，方程组

称为n元齐次线性方程组，当b≠0时，称为n元非齐次线性方程组。

线性方程组的系数和常数项按原位置可以排成数表如下：

对线性方程组的研究，可以转化为对此表的研究。

1.2 矩阵的定义

由$m \times n$个数$a_{ij}（i=1,2,…,m;j=1,2,…,n)$排成的m行n列的数表

称为m行n列的矩阵，简称$m \times n$矩阵，记作

这$m \times n$个数称为矩阵A的元素，简称为元，数$a_{ij}$位于矩阵A的第ｉ行第ｊ列，$m \times n$矩阵A也可记作$A_{m \times n}$。

元素为实数的矩阵称为实矩阵；元素有虚数的矩阵称为复矩阵。

1.2.1 几种特殊的矩阵

（1）行数和列数都等于n的矩阵称为n阶矩阵或n阶方阵，n阶矩阵A也记作$A_n$。

（2）只有一行的矩阵$A=\left(\begin{array}{llll}a_{1} & a_{2} & \cdots & a_{n}\end{array}\right)$称为行矩阵或行向量。

（3）形如以下的矩阵称为对角矩阵（或对角阵），记作$A=\operatorname{diag}\left(\lambda_{1}, \lambda_{2}, \cdots, \lambda_{n}\right)$。

（4）对角阵中的对角线全为1时，此方阵为单位阵。

（5）两矩阵的行数相等，列数也相等时，称它们是同型矩阵。若$A=\left(a_{i j}\right)$与$B=\left(b_{i j}\right)$是同型矩阵，且它们的对应元素相等，即$a_{i j}=b_{i j}(i=1,2, \cdots, m ; j=1,2, \cdots, n)$，则称矩阵A和B相等，记作A=B。

（6）元素都是0 的矩阵称为零矩阵，记作O。

不同型的零矩阵不相等。

行列式和矩阵有本质的区别：

行列式是一个算式，一个数字行列式经过计算得到一个数值，并且行列式的行数和列数一定相等；
而矩阵仅仅是一个数表，它的行数和列数可以不同。

2 矩阵的运算

2.1 矩阵的加法

设有两个$m \times n$矩阵$A=\left(a_{i j}\right)$和$B=\left(b_{i j}\right)$，则矩阵A与B的和记作A＋B，规定为：

注意：两个同型矩阵，才可以相加。

2.2 数与矩阵相乘

数$\lambda$与矩阵$A=\left(a_{i j}\right)$的乘积，简称数乘，记作$\lambda A$或$A\lambda$，规定为

注意：数乘矩阵，需要将这个数乘以该矩阵的每个元素，得到的新矩阵与原矩阵同型。

特别地，当$\lambda=-1$时，将$(-1)A$称为A的负矩阵，记作－A，即：

矩阵的加法和数乘运算统称为矩阵的线性运算。

2.3 线性运算的运算律

设A、B和C均为$m \times n$矩阵，$\lambda$和$\mu$是数，有如下运算规律：

加法交换律：${A}+{B}={B}+{A}$
加法结合律：$(A+B)+C=A+(B+C)$
$A+(-A)=O$
$(\lambda \mu)A=\lambda (\mu A)$
$(\lambda+\mu) A=\lambda A+\mu A$
$\lambda(A+B)=\lambda A+\lambda B$

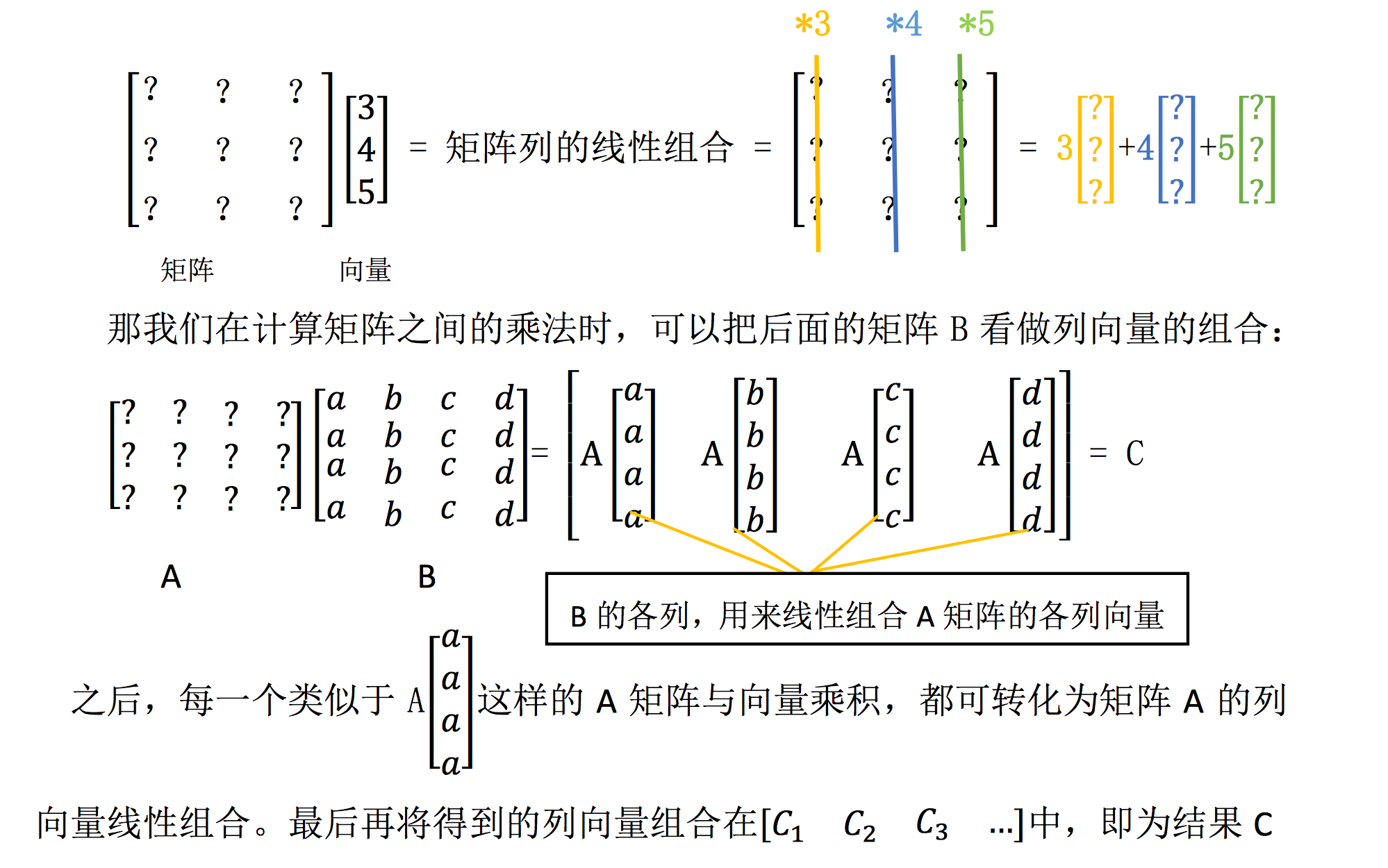
2.4 矩阵的乘法运算

设$A=\left(a_{i j}\right)$是一个$m \times s$矩阵，$B=\left(b_{i j}\right)$是一个$s \times n$矩阵，规定矩阵A与矩阵B的乘法是一个$m \times n$矩阵$C=\left(c_{i j}\right)$，其中

$$
c_{i j}=a_{i 1} b_{1 j}+a_{i 2} b_{2 j}+\cdots+a_{i s} b_{s j}=\sum_{k=1}^{s} a_{i k} b_{k j}
$$

并将此乘积记为$C=AB$。

注意：只有当第一个矩阵A（左矩阵）的列数等于第二个矩阵B（右矩阵）的行数时，两个矩阵才能相乘，并且乘积矩阵AB的行数等于A的行数，而列数等于B的列数。

2.4.1 乘法运算的运算律

设A、B和C均为矩阵，$\lambda$是数，有如下运算规律：

乘法的结合律：$(A B) C=A(B C)$
$\lambda(A B)=A(\lambda B)$
$A(B+C)=A B+A C$
$(B+C) A=B A+C A$

单位矩阵E在矩阵的乘法中的作用，类似于数1在数的乘法中的作用。

由于矩阵的乘法满足结合律，可定义矩阵的幂：设矩阵A是n阶方阵，定义：

$$
A^{1}=A, \quad A^{2}=A^{1} A^{1}, \cdots, \quad A^{k}=A^{k-1} A^{1}
$$

其中k是正整数，即$A^k$是k个A连乘。

特别地，规定$A^{0}=E$，又设$f(x)=a_{0} x^{m}+a_{1} x^{m-1}+\cdots+a_{m-1} x+a_{m}$是关于x的一元m次多项式，则

$$
f(A)=a_{0} A^{m}+a_{1} A^{m-1}+\cdots+a_{m-1} A+a_{m} E
$$

是一个n阶方阵，称为方阵A的m次矩阵多项式。

由于矩阵的乘法不满足交换律，所以以前学过的公式，如平方差公式、和或差的平方公式、和或差的立方公式、立方和或差公式等，均不一定成立。

2.5 矩阵的其他运算

2.5.1 转置运算

将矩阵A的行换成同序数的列得到的矩阵，称为A的转置矩阵，记作$A^T$，即：

矩阵$A^T$的$(i,j)$元就是矩阵A的$(j,i)$元。

转置矩阵也是一种运算，有如下运算律：

$\left(A^{T}\right)^{T}=A$
$(A+B)^{T}=A^{T}+B^{T}$
$(\lambda A)^{T}=\lambda A^{T}$
$(A B)^{T}=B^{T} A^{T}$

同时称满足$A^T=A$的矩阵为对称矩阵。

2.5.2 矩阵的行列式

由n阶方阵A的元素所构成的行列式（各元素的位置不变），称为方阵A的行列式，记作$|A|$或$detA$。

由A确定|A|是一种运算，有如下运算律：

$\left|\boldsymbol{A}^{T}\right|=|\boldsymbol{A}|$，这个相当于使用了行列式的性质，行列式的行和列都是等价的
$|\lambda A|=\lambda^{n}|A|$，相当于对行列式的每一行都乘以一个数，由行列式的性质得，可以把每一行中的这个数给提出来，然后一共有n行，就变成了$\lambda^n$
$|{A} {B}|=|{A}||{B}|$，两个矩阵乘积的行列式等于两个矩阵的行列式的乘积，这个不知道为啥…

2.5.3 伴随矩阵

行列式|A|的各个元素的代数余子式$A_{ij}$所构成的如下矩阵

称为矩阵A的伴随矩阵，简称伴随阵。

余子式和代数余子式的区别是代数余子式带正负号，即$A_{ij}=(-1)^{i+j}M_{ij}$。

设$A^*$是A的伴随矩阵，故$A^{}=A^{} \boldsymbol{A}=|\boldsymbol{A}| E$。

证明：由伴随矩阵的定义可得

2.6 总结

3 逆矩阵

3.1 逆矩阵的概念

对于n阶矩阵A，如果存在一个n阶矩阵B，使得

$$
AB=BA=E
$$

则称矩阵A可逆，并将矩阵B称为A的逆矩阵，简称逆阵。

若A是可逆的，则A的逆矩阵是唯一的。A的逆阵记作$A^{-1}$。

【定理1】若矩阵A可逆，则$|A|\neq0$。

3.2 逆矩阵的求法

若$|A|\neq0$，则矩阵A可逆，且

$$
A^{-1}=\frac{1}{|A|} A^{*}
$$

其中$A^*$为矩阵A的伴随矩阵。

当$|A| = 0$时，矩阵A称为奇异矩阵
当$|A|\neq0$时，矩阵A称为非奇异矩阵

逆阵满足下述运算律：

（1）若A可逆，则$A^{-1}$亦可逆，且

$$
\left(A^{-1}\right)^{-1}=A, \quad\left|A^{-1}\right|=\frac{1}{|A|}
$$

（2）若A可逆，数$\lambda \neq 0$，则$\lambda A$可逆，且

$$
(\lambda A)^{-1}=\frac{1}{\lambda} A^{-1}
$$

（3）若A，B为同阶可逆矩阵，则AB可逆，且$(A B)^{-1}=B^{-1} A^{-1}$

（4）若A可逆，则$A^T$亦可逆，且$\left(A^{T}\right)^{-1}=\left(A^{-1}\right)^{T}$

3.3 逆矩阵的初步应用

设$f(A)=a_{0} A^{m}+a_{1} A^{m-1}+\cdots+a_{m-1} A+a_{m} E$是矩阵A的m次多项式：

（1）若$A=P \Lambda P^{-1}$，则$\boldsymbol{A}^{k}=\boldsymbol{P} \Lambda^{k} P^{-1}$，从而

（2）若$\Lambda=\operatorname{diag}\left(\lambda_{1}, \lambda_{2}, \cdots, \lambda_{n}\right)$为对角阵，则$\Lambda^{k}=\operatorname{diag}\left(\lambda_{1}^{k}, \lambda_{2}^{k}, \cdots, \lambda_{n}^{k}\right)$，从而