线性代数第2章:矩阵及其运算
1 线性方程组和矩阵
1.1 线性方程组
n个未知数m个方程的线性方程组如下:

上述线性方程组的解取决于系数a和常数项b。
当常数项b=0时,方程组

称为n元齐次线性方程组,当b≠0时,称为n元非齐次线性方程组。
线性方程组的系数和常数项按原位置可以排成数表如下:

对线性方程组的研究,可以转化为对此表的研究。
1.2 矩阵的定义
由$m \times n$个数$a_{ij}(i=1,2,…,m;j=1,2,…,n)$排成的m行n列的数表

称为m行n列的矩阵,简称$m \times n$矩阵,记作

这$m \times n$个数称为矩阵A的元素,简称为元,数$a_{ij}$位于矩阵A的第i行第j列,$m \times n$矩阵A也可记作$A_{m \times n}$。
元素为实数的矩阵称为实矩阵;元素有虚数的矩阵称为复矩阵。
1.2.1 几种特殊的矩阵
(1)行数和列数都等于n的矩阵称为n阶矩阵或n阶方阵,n阶矩阵A也记作$A_n$。
(2)只有一行的矩阵$A=\left(\begin{array}{llll}a_{1} & a_{2} & \cdots & a_{n}\end{array}\right)$称为行矩阵或行向量。
(3)形如以下的矩阵称为对角矩阵(或对角阵),记作$A=\operatorname{diag}\left(\lambda_{1}, \lambda_{2}, \cdots, \lambda_{n}\right)$。

(4)对角阵中的对角线全为1时,此方阵为单位阵。

(5)两矩阵的行数相等,列数也相等时,称它们是同型矩阵。若$A=\left(a_{i j}\right)$与$B=\left(b_{i j}\right)$是同型矩阵,且它们的对应元素相等,即$a_{i j}=b_{i j}(i=1,2, \cdots, m ; j=1,2, \cdots, n)$,则称矩阵A和B相等,记作A=B。
(6)元素都是0 的矩阵称为零矩阵,记作O。
不同型的零矩阵不相等。




行列式和矩阵有本质的区别:
- 行列式是一个算式,一个数字行列式经过计算得到一个数值,并且行列式的行数和列数一定相等;
- 而矩阵仅仅是一个数表,它的行数和列数可以不同。
2 矩阵的运算
2.1 矩阵的加法
设有两个$m \times n$矩阵$A=\left(a_{i j}\right)$和$B=\left(b_{i j}\right)$,则矩阵A与B的和记作A+B,规定为:

注意:两个同型矩阵,才可以相加。
2.2 数与矩阵相乘
数$\lambda$与矩阵$A=\left(a_{i j}\right)$的乘积,简称数乘,记作$\lambda A$或$A\lambda$,规定为

注意:数乘矩阵,需要将这个数乘以该矩阵的每个元素,得到的新矩阵与原矩阵同型。
特别地,当$\lambda=-1$时,将$(-1)A$称为A的负矩阵,记作-A,即:

矩阵的加法和数乘运算统称为矩阵的线性运算。
2.3 线性运算的运算律
设A、B和C均为$m \times n$矩阵,$\lambda$和$\mu$是数,有如下运算规律:
- 加法交换律:${A}+{B}={B}+{A}$
- 加法结合律:$(A+B)+C=A+(B+C)$
- $A+(-A)=O$
- $(\lambda \mu)A=\lambda (\mu A)$
- $(\lambda+\mu) A=\lambda A+\mu A$
- $\lambda(A+B)=\lambda A+\lambda B$
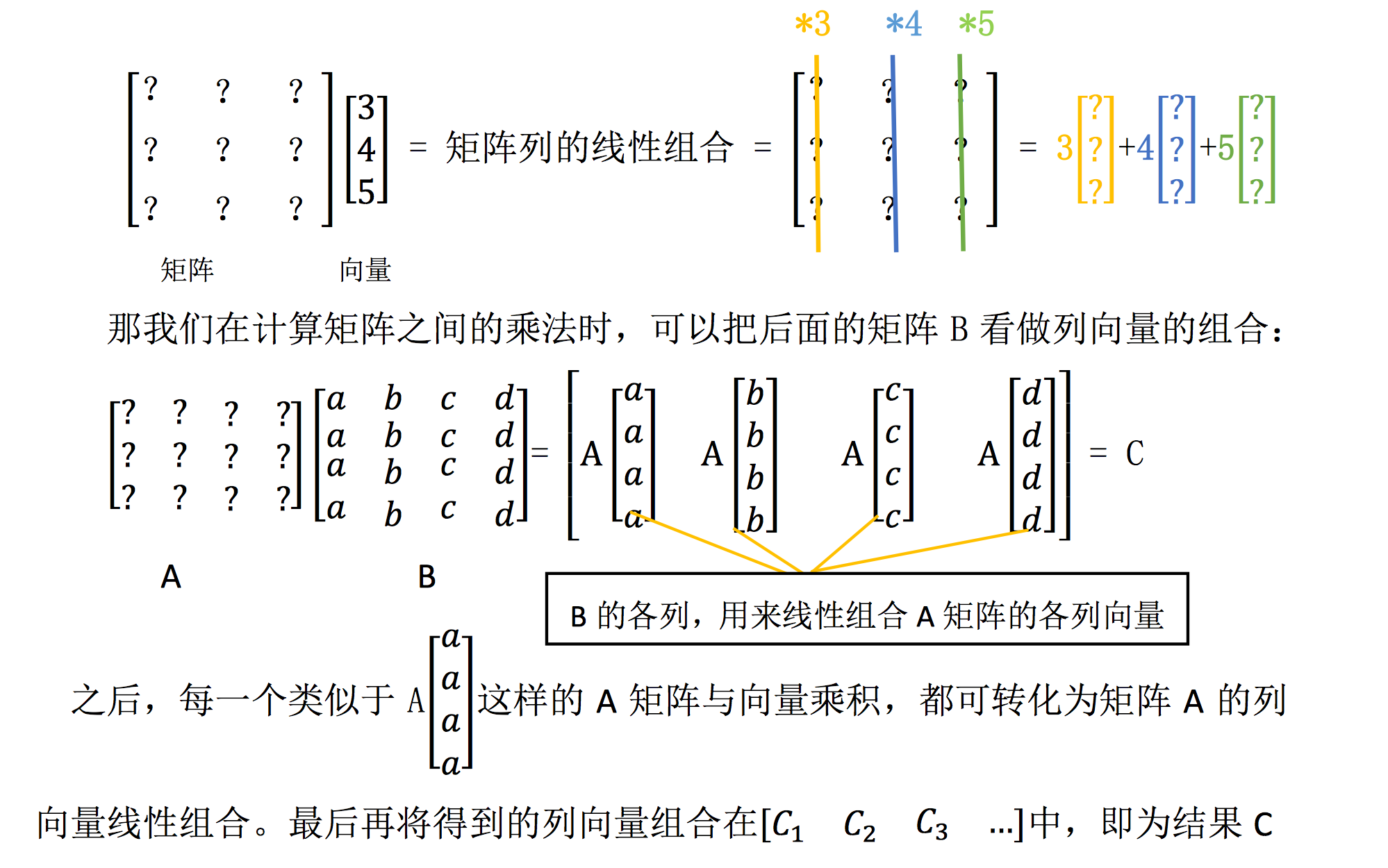
2.4 矩阵的乘法运算
设$A=\left(a_{i j}\right)$是一个$m \times s$矩阵,$B=\left(b_{i j}\right)$是一个$s \times n$矩阵,规定矩阵A与矩阵B的乘法是一个$m \times n$矩阵$C=\left(c_{i j}\right)$,其中
$$
c_{i j}=a_{i 1} b_{1 j}+a_{i 2} b_{2 j}+\cdots+a_{i s} b_{s j}=\sum_{k=1}^{s} a_{i k} b_{k j}
$$
并将此乘积记为$C=AB$。
注意:只有当第一个矩阵A(左矩阵)的列数等于第二个矩阵B(右矩阵)的行数时,两个矩阵才能相乘,并且乘积矩阵AB的行数等于A的行数,而列数等于B的列数。
2.4.1 乘法运算的运算律
设A、B和C均为矩阵,$\lambda$是数,有如下运算规律:
- 乘法的结合律:$(A B) C=A(B C)$
- $\lambda(A B)=A(\lambda B)$
- $A(B+C)=A B+A C$
- $(B+C) A=B A+C A$
单位矩阵E在矩阵的乘法中的作用,类似于数1在数的乘法中的作用。
由于矩阵的乘法满足结合律,可定义矩阵的幂:设矩阵A是n阶方阵,定义:
$$
A^{1}=A, \quad A^{2}=A^{1} A^{1}, \cdots, \quad A^{k}=A^{k-1} A^{1}
$$
其中k是正整数,即$A^k$是k个A连乘。
特别地,规定$A^{0}=E$,又设$f(x)=a_{0} x^{m}+a_{1} x^{m-1}+\cdots+a_{m-1} x+a_{m}$是关于x的一元m次多项式,则
$$
f(A)=a_{0} A^{m}+a_{1} A^{m-1}+\cdots+a_{m-1} A+a_{m} E
$$
是一个n阶方阵,称为方阵A的m次矩阵多项式。
由于矩阵的乘法不满足交换律,所以以前学过的公式,如平方差公式、和或差的平方公式、和或差的立方公式、立方和或差公式等,均不一定成立。

2.5 矩阵的其他运算
2.5.1 转置运算
将矩阵A的行换成同序数的列得到的矩阵,称为A的转置矩阵,记作$A^T$,即:

矩阵$A^T$的$(i,j)$元就是矩阵A的$(j,i)$元。
转置矩阵也是一种运算,有如下运算律:
- $\left(A^{T}\right)^{T}=A$
- $(A+B)^{T}=A^{T}+B^{T}$
- $(\lambda A)^{T}=\lambda A^{T}$
- $(A B)^{T}=B^{T} A^{T}$
同时称满足$A^T=A$的矩阵为对称矩阵。
2.5.2 矩阵的行列式
由n阶方阵A的元素所构成的行列式(各元素的位置不变),称为方阵A的行列式,记作$|A|$或$detA$。
由A确定|A|是一种运算,有如下运算律:
- $\left|\boldsymbol{A}^{T}\right|=|\boldsymbol{A}|$,这个相当于使用了行列式的性质,行列式的行和列都是等价的
- $|\lambda A|=\lambda^{n}|A|$,相当于对行列式的每一行都乘以一个数,由行列式的性质得,可以把每一行中的这个数给提出来,然后一共有n行,就变成了$\lambda^n$
- $|{A} {B}|=|{A}||{B}|$,两个矩阵乘积的行列式等于两个矩阵的行列式的乘积,这个不知道为啥…
2.5.3 伴随矩阵
行列式|A|的各个元素的代数余子式$A_{ij}$所构成的如下矩阵

称为矩阵A的伴随矩阵,简称伴随阵。
余子式和代数余子式的区别是代数余子式带正负号,即$A_{ij}=(-1)^{i+j}M_{ij}$。
设$A^*$是A的伴随矩阵,故$A^{}=A^{} \boldsymbol{A}=|\boldsymbol{A}| E$。
证明:由伴随矩阵的定义可得



2.6 总结

3 逆矩阵
3.1 逆矩阵的概念
对于n阶矩阵A,如果存在一个n阶矩阵B,使得
$$
AB=BA=E
$$
则称矩阵A可逆,并将矩阵B称为A的逆矩阵,简称逆阵。
若A是可逆的,则A的逆矩阵是唯一的。A的逆阵记作$A^{-1}$。
【定理1】若矩阵A可逆,则$|A|\neq0$。
3.2 逆矩阵的求法
若$|A|\neq0$,则矩阵A可逆,且
$$
A^{-1}=\frac{1}{|A|} A^{*}
$$
其中$A^*$为矩阵A的伴随矩阵。
- 当$|A| = 0$时,矩阵A称为奇异矩阵
- 当$|A|\neq0$时,矩阵A称为非奇异矩阵

逆阵满足下述运算律:
(1)若A可逆,则$A^{-1}$亦可逆,且
$$
\left(A^{-1}\right)^{-1}=A, \quad\left|A^{-1}\right|=\frac{1}{|A|}
$$
(2)若A可逆,数$\lambda \neq 0$,则$\lambda A$可逆,且
$$
(\lambda A)^{-1}=\frac{1}{\lambda} A^{-1}
$$
(3)若A,B为同阶可逆矩阵,则AB可逆,且$(A B)^{-1}=B^{-1} A^{-1}$
(4)若A可逆,则$A^T$亦可逆,且$\left(A^{T}\right)^{-1}=\left(A^{-1}\right)^{T}$
3.3 逆矩阵的初步应用
设$f(A)=a_{0} A^{m}+a_{1} A^{m-1}+\cdots+a_{m-1} A+a_{m} E$是矩阵A的m次多项式:
(1)若$A=P \Lambda P^{-1}$,则$\boldsymbol{A}^{k}=\boldsymbol{P} \Lambda^{k} P^{-1}$,从而

(2)若$\Lambda=\operatorname{diag}\left(\lambda_{1}, \lambda_{2}, \cdots, \lambda_{n}\right)$为对角阵,则$\Lambda^{k}=\operatorname{diag}\left(\lambda_{1}^{k}, \lambda_{2}^{k}, \cdots, \lambda_{n}^{k}\right)$,从而





3.4 总结
- 逆矩阵的概念
- 逆矩阵存在的条件
- 逆矩阵的计算
- 待定系数法
- 公式法
- 初等变化法(下一节)
4 克拉默法则
4.1 克拉默法则
之前介绍了使用二阶行列式求解两个二元线性方程组成的方程组,现在进行推广,介绍求解由n个n元线性方程组成的方程组的克拉默法则。
含有n个未知数$x_{1}, x_{2}, \cdots, x_{n}$,n个线性方程的方程组:

与二、三元线性方程组类似,它的解可以用n阶行列式表示,即有若线性方程(1)的系数行列式不等于零,即

那么方程组(1)有唯一解:
$$
x_{1}=\frac{D_{1}}{D}, x_{2}=\frac{D_{2}}{D}, x_{3}=\frac{D_{2}}{D}, \cdots, x_{n}=\frac{D_{n}}{D}
$$
其中$D_{j}(j=1,2, \cdots, n)$是将系数行列式的第j列的元素用方程组右端的常数项代替后,得到的n阶行列式,即:

4.2 重要定理
4.2.1 定理1
若线性方程组(1)的系数行列式$D \neq 0$,则(1)一定有解,且解是唯一的。
4.2.2 定理2
若线性方程组(1)无解或有两个不同的解,则(1)的系数行列式$D=0$。
方程组(1)右端的常数项$b_{1}, b_{2}, \cdots, b_{n}$不全为零时,线性方程组(1)称为非齐次线性方程组;当$b_{1}, b_{2}, \cdots, b_{n}$全为零时,线性方程组(1)称为齐次线性方程组。
对于齐次线性方程组

$x_{1}=x_{2}=\cdots=x_{n}=0$一定是它的解,这个解称为齐次线性方程组(2)的零解;若存在一组不全为零的数是(2)的解,称其为(2)的非零解。

4.2.3 定理3
若线性方程组(2)的系数行列式$D \neq 0$,则(2)只有零解,没有非零解。
4.2.4 定理4
若线性方程组(2)有非零解,则(2)的系数行列式$D=0$。
4.3 总结
(1)利用克拉默法则解线性方程组的条件:
- 方程的个数=未知数的个数
- 系数行列式$D \neq 0$
(2)对非齐次线性方程组

(3)对齐次线性方程组

5 矩阵分块法
5.1 矩阵的分块
对于行数和列数较高的矩阵A,运算有时会采用分块法,使大矩阵的运算转化成小矩阵的运算。
将矩阵A用若干条纵线和横线分成许多小矩阵,每个小矩阵称为A的子块,以子块为元素的形式上的矩阵称为分块矩阵。

5.2 分块矩阵的运算规则
分块矩阵的运算规则与普通矩阵的运算规则类似。
(1)设矩阵A与B的行数相同、列数也相同,采用相同的分块法,有

其中$A_{ij}$与$B_{ij}$的行数相同、列数也相同,则

(2)设$A=\left(\begin{array}{ccc}A_{11} & \cdots & A_{1 r} \ \vdots & & \vdots \ A_{s 1} & \cdots & A_{s r}\end{array}\right)$,$\lambda$为数,则



(4)设$A=\left(\begin{array}{ccc}A_{11} & \cdots & A_{1 r} \ \vdots & & \vdots \ A_{s 1} & \cdots & A_{s r}\end{array}\right)$,则

(5)设A是n阶矩阵,若A的分块矩阵只有在对角线上有非零子块,其余子块均为零矩阵,且在对角线上的子块都是方阵,即

其中$A_{i}(i=1,2, \cdots, s)$都是方阵,称A为分块对角阵。分块对角阵的行列式有下述性质:
$$
|A|=\left|A_{1}\right|\left|A_{2}\right| \cdots\left|A_{s}\right|
$$
由此可知,若$\left|A_{i}\right| \neq 0(i=1,2, \cdots, s)$,有