1 随机样本

1.1 总体

对有关对象的某一数量指标进行试验和观察，将试验的全部可能的观察值称为总体；

每一个可能的观察值称为个体，个体的数量称为总体的容量。

一个总体对应一个随机变量X；随机变量的分布函数和数字特征称为总体X的分布函数和数字特征。

1.2 样本

总体分布一般是未知的，或只知道是包含未知参数的分布。通过从总体中抽取一部分个体，根据获得的数据推断总体分布，这一抽取过程称为 “抽样”，所抽取的部分个体称为总体的一个样本. 样本中所包含的个体数目称为样本容量.

从总体抽取一个个体：对总体X进行一次观察并记录结果。

定义：设X是具有分布函数F的随机变量，若$X_{1}, X_{2}, \ldots, X_{\mathrm{n}}$是具有同一分布F的且相互独立的随机变量，则$X_{1}, X_{2}, \ldots, X_{\mathrm{n}}$为从总体X(总体F)得到的容量为n的简单随机样本，简称样本。

观察值$X_{1}, X_{2}, \ldots, X_{\mathrm{n}}$为样本值，又称为X的n个独立观察值。

“简单随机抽样”特点：$X_{1}, X_{2}, \ldots, X_{\mathrm{n}}$相互独立且每一个与所考察的总体有相同的分布.

$\left(X_{1}, X_{2}, \ldots, X_{n}\right)$分布函数与联合概率密度函数满足：

$F^{*}\left(x, x_{2}, \ldots, x_{n}\right)=F\left(x_{1}\right) F\left(x_{2}\right) \ldots F\left(x_{n}\right)$
$f^*\left(x,x_2,\ldots,x_n\right)=f\left(x_1\right)f\left(x_2\right)\ldots f\left(x_n\right)$

2 抽样分布

2.1 统计量与经验分布函数

定义：设$X_{1}, X_{2}, \ldots, X_{\mathrm{n}}$是来自总体X的一个样本，$g(X_{1}, X_{2}, \ldots, X_{\mathrm{n}})$是$X_{1}, X_{2}, \ldots, X_{\mathrm{n}}$的函数，若g中不含未知参数，则称$g(X_{1}, X_{2}, \ldots, X_{\mathrm{n}})$是一个统计量。

$g\left(x_{1}, x_{2}, \cdots, x_{n}\right)$是统计量$g(X_{1}, X_{2}, \ldots, X_{\mathrm{n}})$的观察值。

2.1.1 几个常见的统计量

2.1.1.1 样本平均值

$$
\bar{X}=\frac{1}{n} \sum_{i=1}^{n} X_{i}
$$

2.1.1.2 样本方差

$$
S^{2}=\frac{1}{n-1} \sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2}=\frac{1}{n-1}\left(\sum_{i=1}^{n} X_{i}^{2}-n \bar{X}^{2}\right)
$$

2.1.1.3 样本标准差

$$
S=\sqrt{\frac{1}{n-1} \sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2}}
$$

2.1.1.4 样本k阶原点矩

$$
A_{k}=\frac{1}{n} \sum_{i=1}^{n} X_{i}^{k} \quad k=1,2, \ldots
$$

2.1.1.5 样本k阶中心矩

$$
B_k=\frac1n\sum_{i=1}^n\left(X_i-\overline{X}\right)^k
$$

2.1.2 统计量的观察值

定理：若总体X的k阶矩$E\left(X^{k}\right)=\mu_{k}$存在，则当$n \rightarrow \infty$时，$A_{k} \xrightarrow{P} \mu_{k}(k=1,2, \cdots)$

结论：设$X_{1}, X_{2}, \ldots, X_{\mathrm{n}}$是来自总体X的一个样本，则$E(X)=\mu$，即：

$$
E\left(A_{1}\right)=E\left(\frac{1}{n} \sum_{i=1}^{n} X_{i}\right)=E(X)=\mu
$$

2.2 统计三大抽样分布

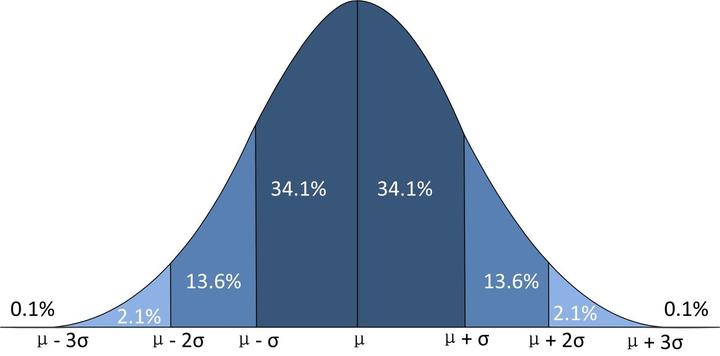
统计量的分布称为抽样分布，来自正态总体的三个常用统计量的分布：$\chi^{2}$（卡方）分布、t分布和F分布。

$2.2.1 \chi^{2}

$分布

定义：设$X_{1}, X_{2}, \ldots, X_{\mathrm{n}}$相互独立，都服从正态分布N(0, 1)，则称随机变量

$$
\chi^{2}=X_{1}^{2}+X_{2}^{2}+\cdots+X_{n}^{2}
$$

服从自由度为n的$\chi^{2}$分布，记为$\chi^{2} \sim \chi^{2}(n)$。

$\chi^{2}(n)$分布的概率密度为：

$\chi^{2}(n)$分布的概率密度图像为：

$2.2.1.1 \chi^{2}$分布的分位点

对于给定的正数α，0<α<1，称满足以下条件的点$\chi_{\alpha}^{2}(n)$为$\chi^{2}(n)$分布的上α分位点。

$$
P{\chi^{2}>\chi_{\alpha}^{2}(n)}=\int_{\chi_{\alpha}^{2}(n)}^{\infty} f(y) \mathrm{d} y=\alpha
$$

当n充分大时，$\chi_{\alpha}^{2}(n) \approx \frac{1}{2}\left(z_{\alpha}+\sqrt{2 n-1}\right)^{2}$，其中$\boldsymbol{z}_{\alpha}$是正态分布的上α分位点。

2.2.2 t 分布

设$X \sim N(0,1), Y \sim \chi^{2}(n)$，且X，Y独立，则随机变量$t=\frac{X}{\sqrt{Y / n}}$服从自由度为n的t分布，记为$t \sim t(n)$，t分布又称学生氏分布。

t(n)分布的概率密度函数为：

$$
h(t)=\frac{\Gamma\left(\frac{n+1}{2}\right)}{\sqrt{\pi n} \Gamma\left(\frac{n}{2}\right)}\left(1+\frac{t^{2}}{n}\right)^{-\frac{n+1}{2}}-\infty<t<+\infty
$$

2.2.2.1 t分布的性质

（1）具有自由度为n的t分布t~t(n)，其数学期望与方差为：$E(t)=0, D(t)=n /(n-2)$

（2）t分布的概率密度函数关于t=0对称，即当n足够大时，满足$t \stackrel{\text { 近似 }}{\sim} N(0,1)$，即$\lim _{n \rightarrow \infty} h(t)=\frac{1}{\sqrt{2 \pi}} e^{\frac{-t^{2}}{2}}$

t(n) 分布的概率密度曲线如下图所示：

（3）t分布的分位点：对于给定的α，0<α<1，称满足条件$P{t>t_{\alpha}(n)}=\int_{t_{\alpha}(n)}^{\infty} h(t) d t=\alpha$的点称为t(n)分布的上α分位点，如图所示：

t分布的上α分位点的性质：$t_{1-\alpha}(n)=-t_{\alpha}(n)$；当n>45时，$t_{\alpha}(n) \approx z_{\alpha}$。

2.2.3 F分布

$F\left(n_{1}, n_{2}\right)$分布的概率密度为：

$$
\psi(y)=\begin{cases}&\frac{\Gamma\left(\frac{n_1+n_2}{2}\right)\left(\frac{n_1}{n_2}\right)^{\frac{n_1}{2}}y^{\frac{n_1}{2}-1}}{\Gamma\left(\frac{n_1}{2}\right)\Gamma\left(\frac{n_2}{2}\right)\left[1+\left(\frac{n_1y}{n_2}\right)\right]^{\frac{n_1+n_2}{2}}},&y>0,\&0,&\text{其他}.\end{cases}
$$

F分布的概率密度曲线如图

2.2.3.1 F分布的性质

（1）如果$ \mathbf{F}\sim\mathbf{F}\left(\mathbf{n}_1,\mathbf{n}_2\right) $，那么$\frac{1}{\mathbf{F}} \sim F (\mathbf{n}_2,\mathbf{n}_1)$

（2）F分布的数学期望为：

$$
\mathbf{E}(\mathbf{F})=\frac{\mathbf{n}_2}{n_2-2}\quad\text{若}n_2>2
$$

（3）F分布的分位数：对于给定的α，0<α<1，称满足条件

$$
P{F>F_{\alpha}(n_{1}, n_{2})}=\int_{F_{\alpha}(n_{1}, n_{2})}^{\infty} \phi(y) d y=\alpha
$$

的点$F_{\alpha}\left(n_{1}, n_{2}\right)$为$F\left(n_{1}, n_{2}\right)$分布的上α分位点，如图所示：

F分布的上α分位点的性质：$F_{1-\alpha}\left(n_{1}, n_{2}\right)=\frac{1}{F_{\alpha}\left(n_{2}, n_{1}\right)}$

F分布的上α分位数可查表求得，如下所示：

$$
F_{0.95}(12,9)=\frac{1}{F_{0.05}(9,12)}=\frac{1}{2.80}=0.357
$$

2.3 正态总体的样本均值和样本方差的分布

设总体X（不管服从什么分布，只要均值和方差存在）的均值为$\mu$，方差为$\sigma^{2}$，$X_{1}, X_{2}, \ldots, X_{\mathrm{n}}$是来自X的一个样本，X，S²分别是样本均值和样本方差，则有：

$$
E(\bar{X})=\mu, D(\bar{X})=\sigma^{2} / n, \quad E\left(S^{2}\right)=\sigma^{2}
$$

2.3.1 定理1

定理1是关于样本均值的分布

设$X_{1}, X_{2}, \ldots, X_{\mathrm{n}}$是来自正态总体$N\left(\mu, \sigma^{2}\right)$的样本，$\overline{X}$是样本均值，则有：

$$
X \sim N\left(\mu, \frac{\sigma^{2}}{n}\right) \quad 即 \frac{\bar{X}-\mu}{\sigma / \sqrt{n}} \sim N(0,1)
$$

2.3.2 定理2

定理2是关于样本方差的分布

设$X_{1}, X_{2}, \ldots, X_{\mathrm{n}}$是来自正态总体$N\left(\mu, \sigma^{2}\right)$的样本，$\overline{X}$是样本均值，S²是样本方差，则有：

$\frac{(n-1) S^{2}}{\sigma^{2}} \sim \chi^{2}(n-1)$
$\overline{X}$与S²独立

该定理主要适用于总体均值$\mu$未知的情况。

2.3.3 定理3

设$X_{1}, X_{2}, \ldots, X_{\mathrm{n}}$是来自正态总体$N\left(\mu, \sigma^{2}\right)$的样本，$\overline{X}$是样本均值，S²是样本方差，则有：

$$
\frac{\bar{X}-\mu}{S / \sqrt{n}} \sim t(n-1)
$$

主要适用于总体方差$\sigma^{2}$未知的情况。

2.3.4 定理4

该定理是关于两总体样本均值差、样本方差比的分布

设$X \sim N\left(\mu_{1}, \sigma_{1}^{2}\right)$，$Y \sim N\left(\mu_{2}, \sigma_{2}^{2}\right)$，且X与Y独立，$X_{1}, X_{2}, \ldots, X_{\mathrm{n1}}$是来自X的样本，$Y_{1}, Y_{2}, \ldots, Y_{\mathrm{n2}}$是来自Y的样本，$\overline{X}$和$\overline{Y}$分别是这两个样本的样本均值，$S_{1}^{2}$和$S_{2}^{2}$分别是这两个样本的样本方差，则有：

$$
\frac{(\bar{X}-\bar{Y})-(\mu_1-\mu_2)}{S_w\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}\sim t (n_1+n_2-2)
$$

当$\sigma_{1}^{2}=\sigma_{2}^{2}=\sigma^{2}$时，有

$$
\frac{(\bar{X}-\bar{Y})-\left(\mu_{1}-\mu_{2}\right)}{S_{w} \sqrt{\frac{1}{n_{1}}+\frac{1}{n_{2}}}} \sim t\left(n_{1}+n_{2}-2\right),
$$

$$
其中 S_{w}^{2}=\frac{\left(n_{1}-1\right) S_{1}^{2}+\left(n_{2}-1\right) S_{2}^{2}}{n_{1}+n_{2}-2}, \quad S_{w}=\sqrt{S_{w}^{2}}.
$$