1 随机试验

概率论是研究随机现象规律性的一门数学学科。

1.1 随机现象

随机现象的特征：条件不能完全决定结果。

1.1.1 确定性现象

在一定条件下必然发生的现象称为确定性现象。

1.1.2 随机现象

在一定条件下可能出现也可能不出现的现象称为随机现象。

实例1：在相同条件下掷一枚均匀的硬币，观察正反两面出现的情况。

说明：

随机现象揭示了条件和结果之间的非确定性联系 , 其数量关系无法用函数加以描述
随机现象在一次观察中出现什么结果具有偶然性, 但在大量试验或观察中, 这种结果的出现具有一定的统计规律性

随机现象是通过随机试验来研究的。

1.2 随机试验

在概率论中，把具有以下三个特征的试验称为随机试验。

可以在相同的条件下重复地进行
每次试验的可能结果不止一个, 并且能事先明确试验的所有可能结果
进行一次试验之前不能确定哪一个结果会出现

说明：

随机试验简称为试验, 是一个广泛的术语。它包括各种各样的科学实验, 也包括对客观事物进行的 “调查”、“观察”或 “测量” 等
随机试验通常用 E 来表示

2 样本空间、随机事件

2.1 样本空间、样本点

一个随机试验E的所有可能结果所组成的集合称为随机试验E的样本空间，记为S。样本空间中的元素，即E的每个结果，称为样本点。

实例1 将一枚硬币抛掷两次, 观察正面H、反面T出现的情况。

则样本空间：$S={(H,H), (H,T), (T,H), (T,T)}$

试验不同, 对应的样本空间也不同.
同一试验, 若试验目的不同, 则对应的样本空间也不同.
建立样本空间, 事实上就是建立随机现象的数学模型。因此 , 一个样本空间可以概括许多内容大不相同的实际问题.

2.2 随机事件的概念

随机试验 E 的样本空间 S 的子集称为 E 的随机事件, 简称事件。通常以大写英文字母 A, B, C, 来表示事件。

当且仅当集合A中的一个样本点出现时, 称随机事件A发生.
随机试验、样本空间与随机事件的关系：每一个随机试验相应地有一个样本空间, 样本空间的子集就是随机事件。

2.3 事件间的关系与事件的运算

2.3.1 随机事件的运算规律

幂等律：$A \cup A=A, \quad A \cap A=A$
交换律：$A \cup B=B \cup A, \quad A \cap B=B \cap A$
结合律：

$$
\begin{array}{l}(A \cup B) \cup C=A \cup(B \cup C) \ (A \cap B) \cap C=A \cap(B \cap C)\end{array}
$$

分配律：

$$
\begin{array}{l}A \cap(B \cup C)=(A \cap B) \cup(A \cap C) \ A \cup(B \cap C)=(A \cup B) \cap(A \cup C)\end{array}
$$

德摩根定律：

$$
\overline{A \cup B}=\bar{A} \cap \bar{B}, \overline{A \cap B}=\bar{A} \cup \bar{B}
$$

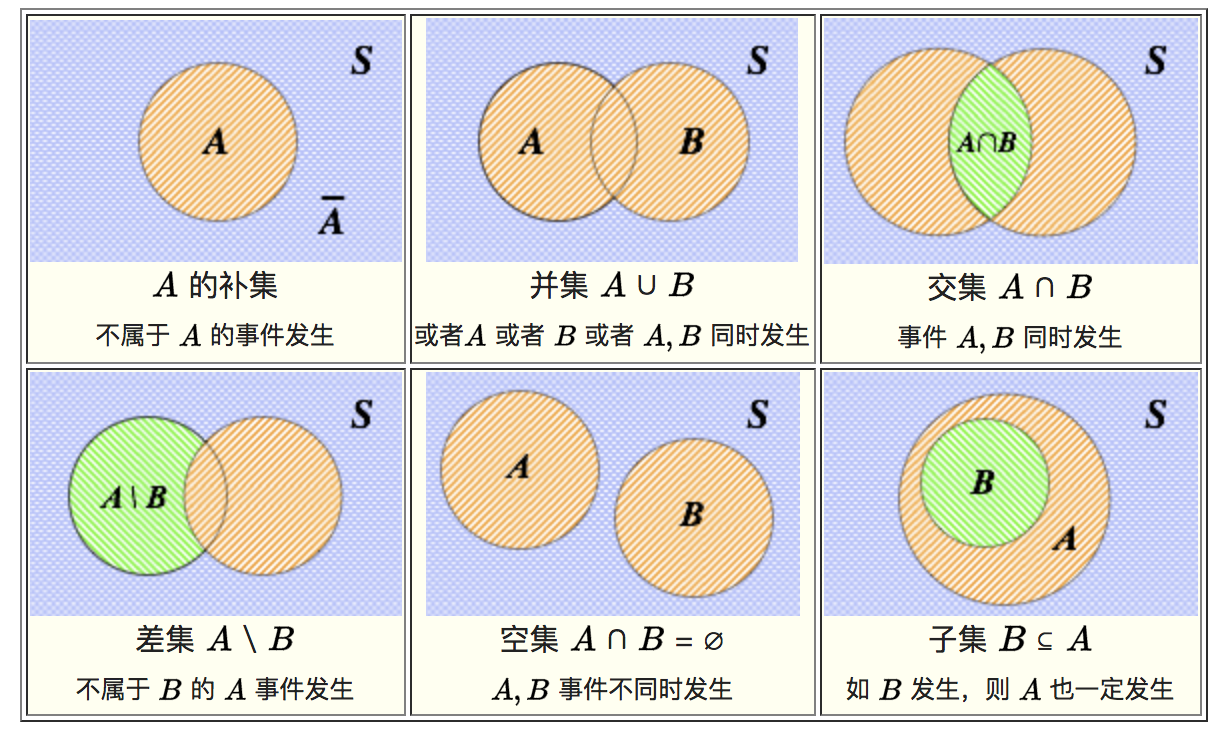
2.3.2 概率论与集合论之间的对应关系

3 频率与概率

3.1 频率的定义与性质

3.1.1 定义

在相同的条件下，共进行了n次试验，在这n次试验中，事件A发生的次数$n_A$称为事件A发生的频数。比值$\frac{n_{A}}{n}$称为事件A发生的频率，并记成$f_{n}(A)$。

3.1.2 性质

设 A 是随机试验 E 的任一事件, 则有

$0 \leq f_{n}(A) \leq 1$
$f_{n}(S)=1$
$若 A_{1}, A_{2}, \ldots, A_{k} 是两两互不相容的事件, 则$

$$
f_{n}\left(A_{1} \cup A_{2} \cup \ldots \cup A_{k}\right)=f_{n}\left(A_{1}\right)+f_{n}\left(A_{2}\right)+\ldots+f_{n}\left(A_{k}\right)
$$

例1 将一枚硬币抛掷 5 次、50 次、500 次, 各做7 遍, 观察正面出现的次数及频率.

随n的增大, 频率 f 呈现出稳定性。可见，在大量重复的试验中, 随机事件出现的频率具有稳定性. 即通常所说的统计规律性。

3.2 概率的定义与性质

1933年, 苏联数学家柯尔莫哥洛夫（Kolmogorov）提出了概率论的公理化结构, 给出了概率的严格定义, 使概率论有了迅速的发展.

3.2.1 概率的公理化定义

设E是随机试验，S是它的样本空间，对于E的每一个事件A赋予一个实数 $P(A)$，称之为事件A的概率，如果它满足下列三个条件：

$P(A) \geq 0 $（非负性）
$P(S)=1$（规范性）
对于两两互斥是将$A_1,A_2,…$，有可列可加性：

$$
P(A_1+A_2+…) = P(A_1) + P(A_2)+ \cdots
$$

3.2.2 概率的性质

$P(\varnothing)=0$
$若 A_{1}, A_{2}, \ldots, A_{n} 是两两互不相容的事件则有$

$$
P\left(A_{1} \cup A_{2} \cup \cdots \cup A_{n}\right)=P\left(A_{1}\right)+P\left(A_{2}\right)+\cdots+P\left(A_{n}\right)
$$

$设 A, B 为两个事件,且 A \subset B, 则P(A) \leq P(B), \quad P(B-A)=P(B)-P(A) .$
$对于任一事件 A, P(A) \leq 1.$
$设 \bar{A} 是 A 的对立事件, 则 P(\bar{A})=1-P(A).$
$(加法公式)对于任意两事件 A, B，有P(A \cup B)=P(A)+P(B)-P(A B) .$

三个事件和的情况：

$$
\begin{aligned} & P\left(A_{1} \cup A_{2} \cup A_{3}\right) = {P}\left(A_{1}\right)+{P}\left(A_{2}\right)+{P}\left(A_{3}\right)-{P}\left(A_{1} A_{2}\right)-{P}\left(A_{2} A_{3}\right)- {P}\left(A_{1} A_{3}\right)+{P}\left(A_{1} A_{2} A_{3}\right) .\end{aligned}
$$