1 串的存储

1.1 定长顺序存储表示

1
2
#define MAXSTRING 255  // 用户可在255以内定义最大串长
typedef unsigned char SString [ MAXSTRLEN +1 ];

1.2 堆分配存储表示

存储空间是在程序执行过程中动态分配得到的，在堆中使用malloc函数和free函数完成动态存储管理。

1
2
3
4
5
typedef struct
{
	char *Ch;    // 若是非空串，则按串长分配存储区，否则ch为NULL
	int Length;  // 串长度
}HString;

1.3 块链存储表示

类似于线性表的链式存储结构，也可采用链表方式存储串值。

每个结点既可放一个字符，也可以存放多个字符，每个结点称为块，整个链表称为块链结构。

块链的效率：

  • 每个结点中数据域越大，效率越高。

$$
存储密度 = \frac{串所占的存储位}{实际分配的存储位}
$$

1
2
3
4
5
6
7
8
9
10
11
#define CHUNKSIZE 80  // 块大小
typedef struct Chunk
{
	char ch[CHUNKSIZE];
	struct Chunk *Next;
}Chunk;
typedef struct
{
	Chunk *Head, *Tail;	 // 头指针和尾指针
	int Length;              //串的长度
}LString;

2 串的模式匹配

2.1 简单的模式匹配算法

子串的定位操作通常称作串的模式匹配（其中T被称模式串），是各种串处理系统中最重要的操作之一。

2.1.1 基本思想

  1. 从主串S的第一个字符起和模式的第一个字符比较之
    • 若相等，则继续逐个比较后续字符
    • 否则从主串的下一个字符起再重新和模式的字符比较之
  2. 依次类推，直至模式T中的每个字符依次和主串S中的一个连续的字符序列相等，则称匹配成功
1
2
3
4
5
6
7
8
9
10
11
int BF(string S, string T)
{
	int i = 0, j = 0;
	while (i < S.size() && j < T.size())
	{
		if (S[i] == T[j]) i ++, j ++;
		else i = i - j + 2, j = 0;
	}
	if (j >= T.size()) return i - T.size();
	return 0;
}

2.1.2 算法演示

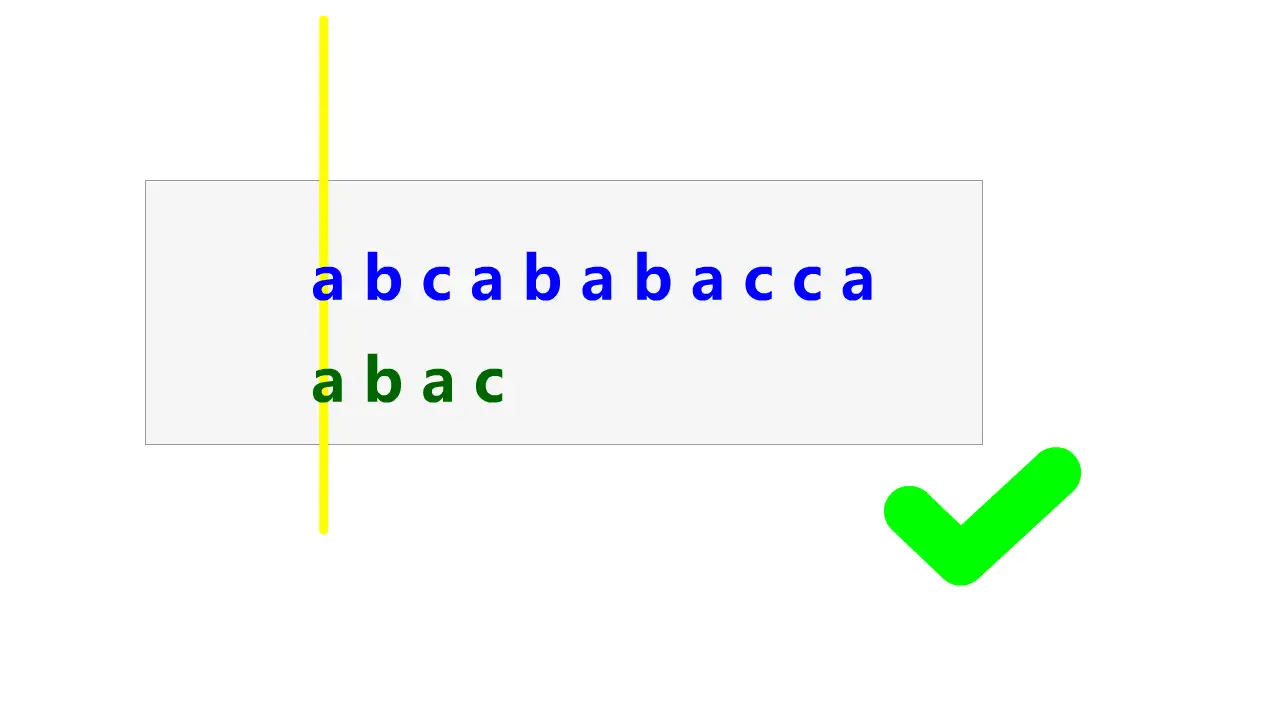
2.1.3 性能分析

  • 最好时间复杂度：O(T.size() + S.size())
  • 最坏时间复杂度：O(T.size() * S.size())

2.2 KMP算法

KMP算法的改进在于：每一趟匹配过程中出现字符比较不等时，不需要回朔指针 i ，要利用已经“部分匹配”结果，调整指针 j ，即将模式向右滑动尽可能远的一段距离，来提高算法效率。

KMP算法匹配过程示意如下：

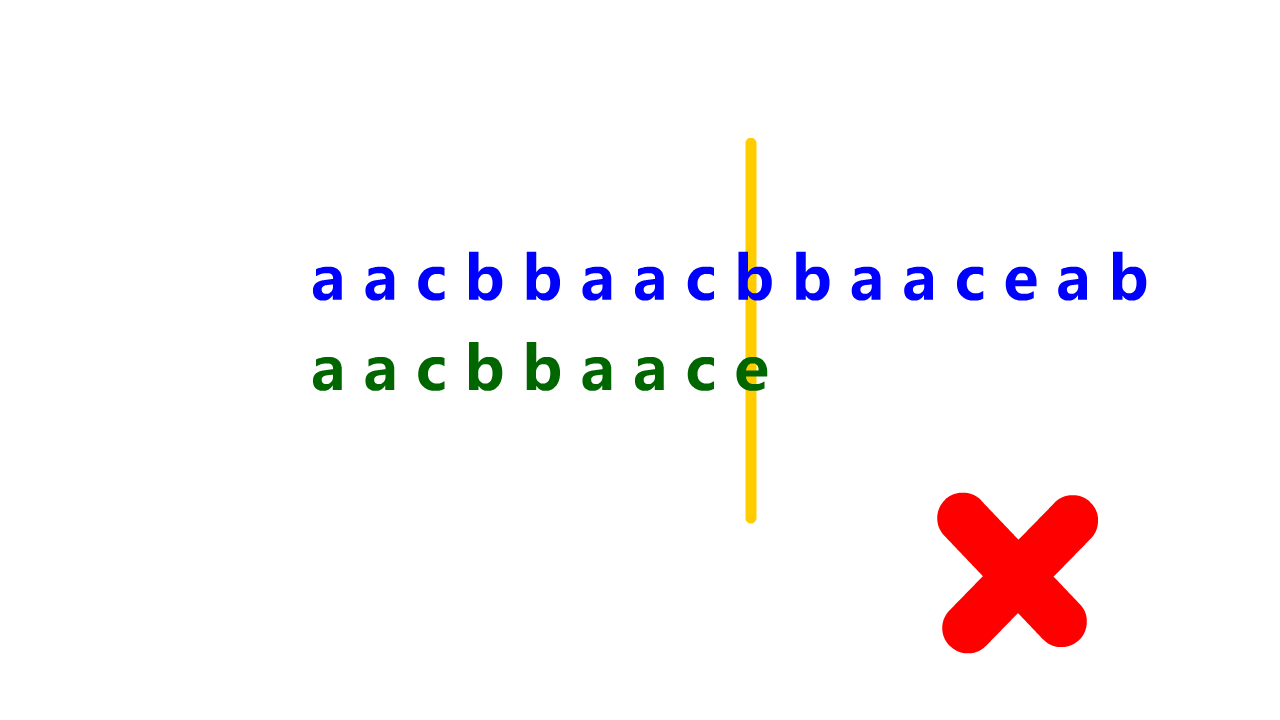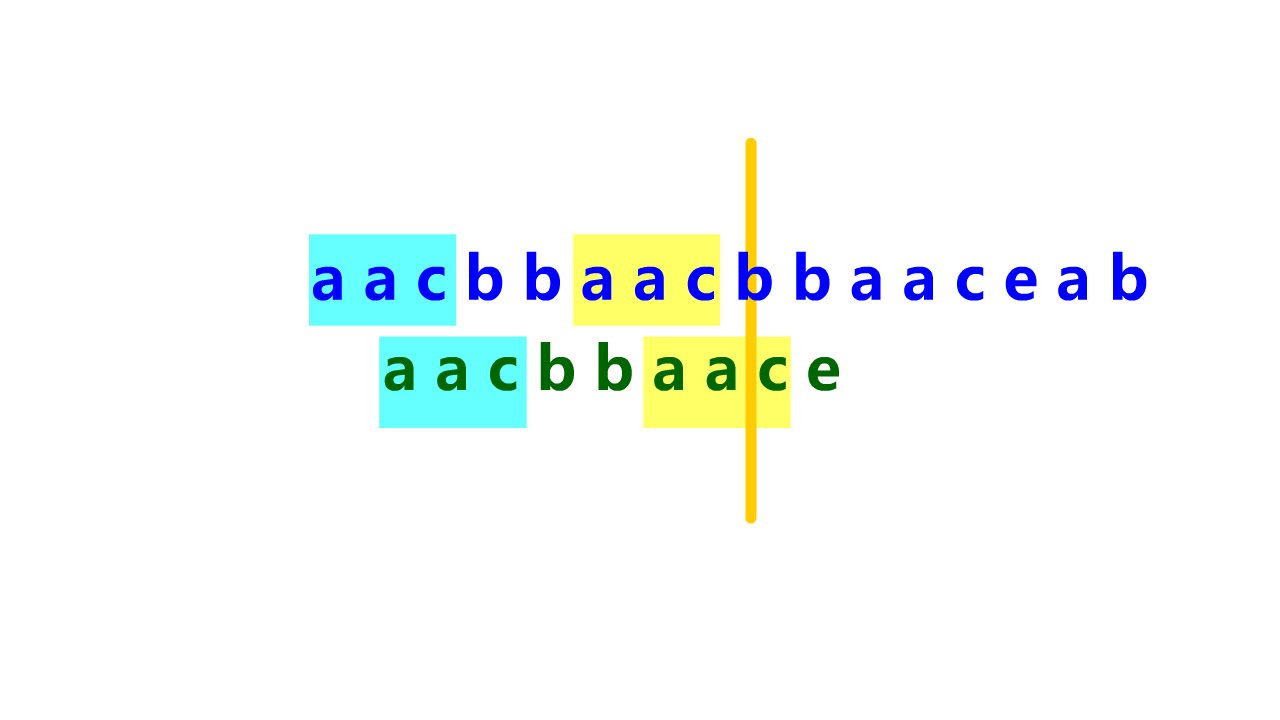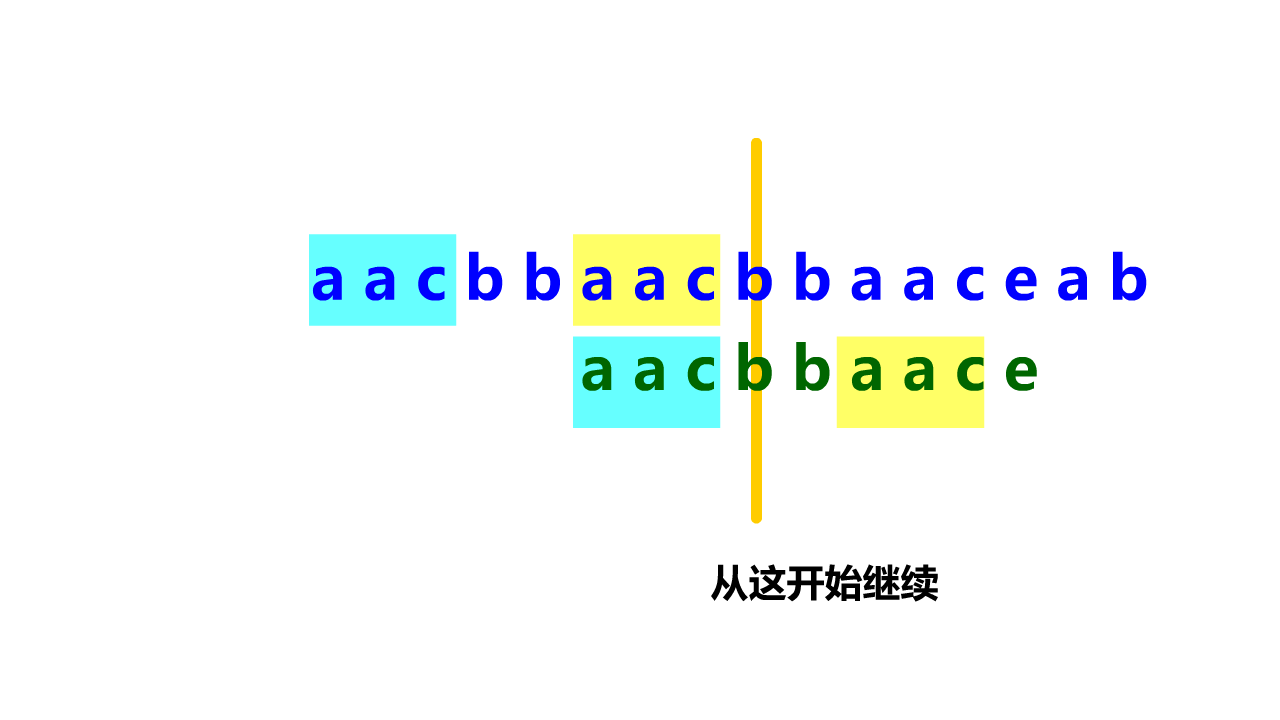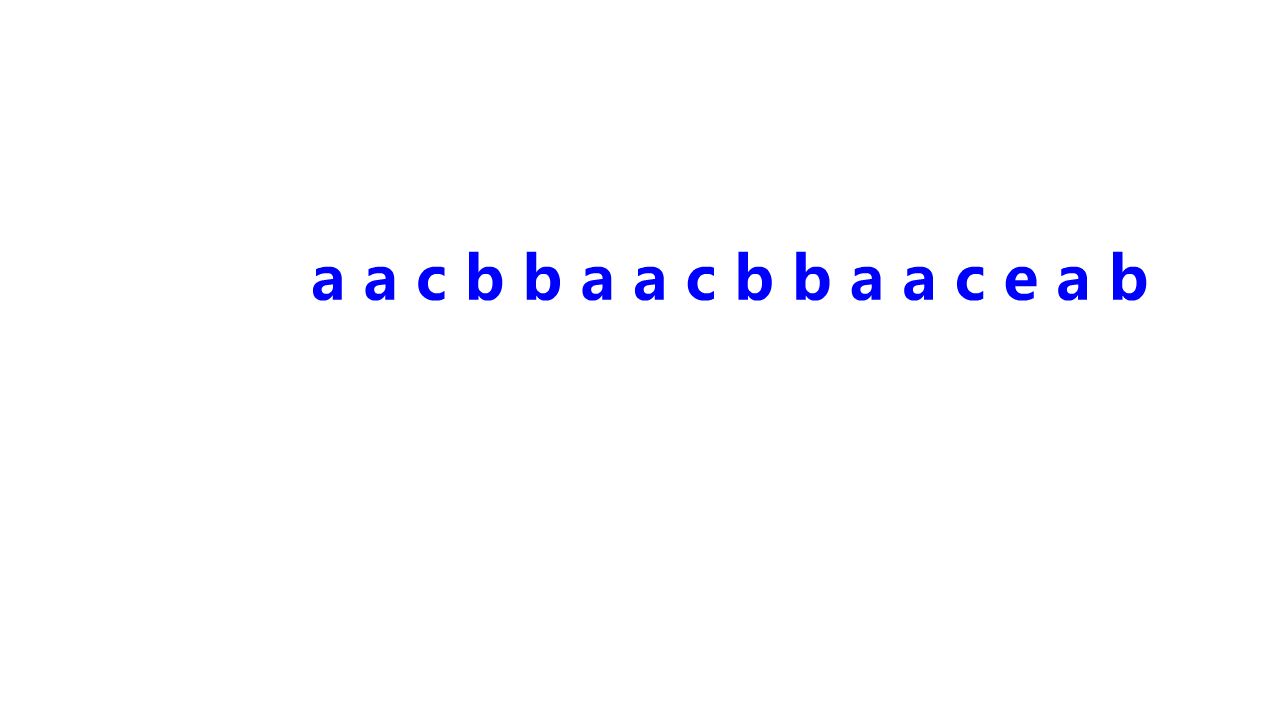
前缀表是用来回退的，它记录了模式串与主串(文本串)不匹配的时候，模式串应该从哪里开始重新匹配。

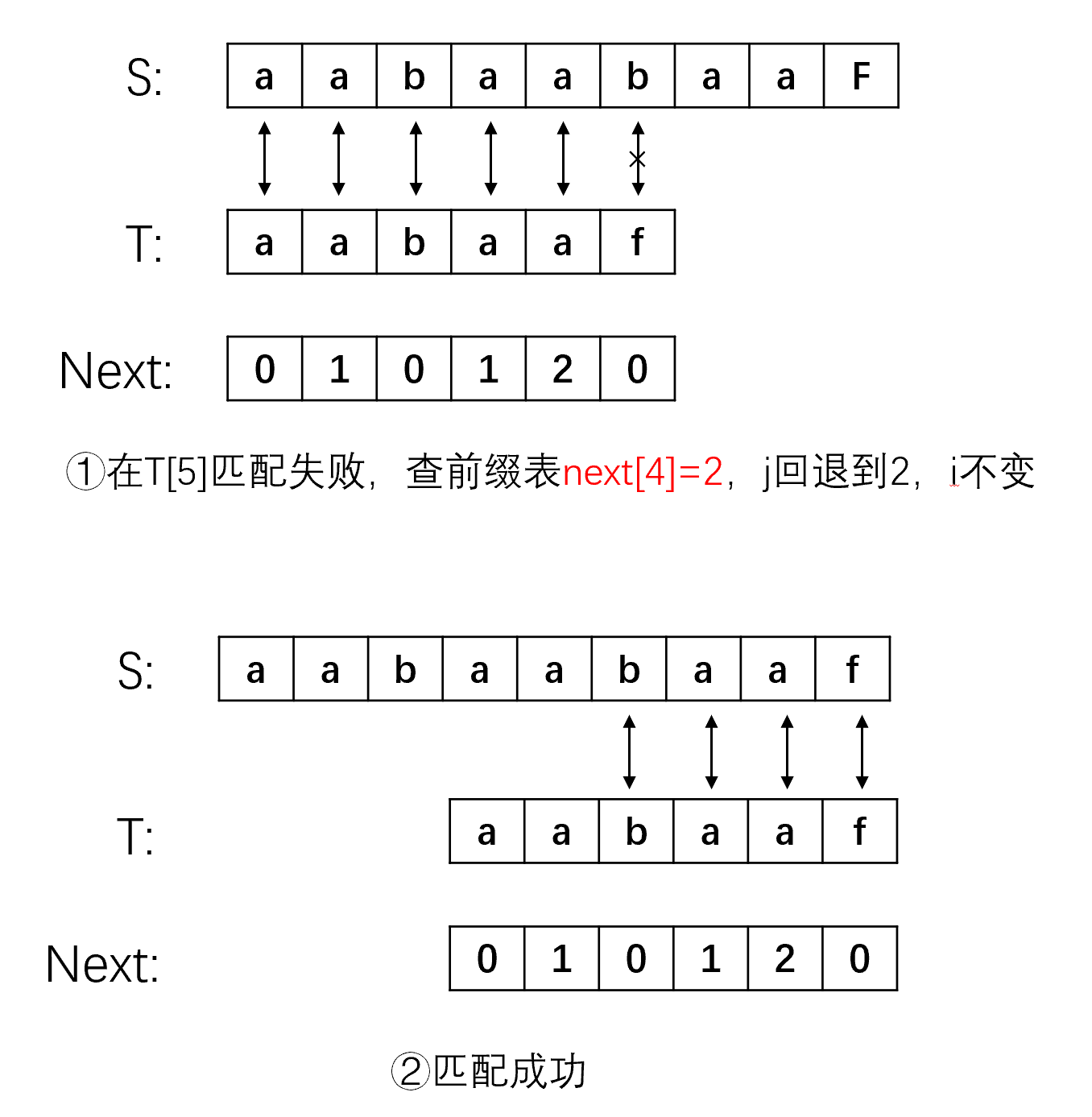
从上面的流程可以看到，在子串的某一个字符 t[j] 处匹配失败时，我们需要查找该字符前面的那个子串的最大相等前后缀的长度，即 next[j-1] ，然后使 j 指针退回到 next[j-1] ，i 指针不变，继续匹配，不断重复这个操作知道匹配成功或者 j 指针大于等于子串长度。

在这里j指针之所以退回到 next[j-1] 的位置我们可以根据例子思考一下，字符”f”前面的子串为”aabaa”，该子串的最大相等前后缀为”aa”，而该子串的后缀”aa”已经与 s[3]s[4] 比较过是相等的，那么子串的前缀就一定是与 s[3]s[4] 相等的，不需要比较，因此我们的 j 可以从前缀的后面第一个字符开始匹配，而前缀的长度为 next[j-1]，所以j应该回退到 next[j-1]。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
int ne[N];

void get_next()
{
	for (int i = 2, j = 0; i <= n; i ++)
	{
		while (j && p[i] != p[j + 1]) j = ne[j];
		if (p[i] == p[j + 1]) j ++;
		ne[i] = j;
	}
}

int kmp()
{
	for (int i = 1, j = 0; i <= m; i ++)
	{
		while (j && s[i] != p[j + 1]) j = ne[j];
		if (s[i] == p[j + 1]) j ++;
		if (j == n)
		{
			cout << i - n << " ";
			j = ne[j];
		}
	}
}

2.2.1 性能分析

  • KMP算法的时间复杂度是O(n + m)，主串始终没有回退
  • 但在一般的情况下，普通模式匹配的实际执行时间近似为O(n + m)，因此至今仍然被采用
  • KMP算法尽在主串与子串有很多“部分匹配”时才显得比普通算法快得多，主要优点是主串不回溯

2.3 KMP算法的进一步优化

在进行匹配时，当 $p_{j} ≠ s_{j}$时，下次匹配必然是 $p_{next[j]}$ 和 $s_{j}$ 进行比较，如果$p_{next[j]} = p_{j}$，那么就相当于拿了一个和 $p_{j}$ 相等的字符和 $s_{j}$ 继续比较，这必然导致继续失配。

如果出现了，则需要再次递归，将 next[j] 修正为 next[next[j]] ，直至两者不相等为止，更新后的数组命名为 nextval ，计算 next 数组修正如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
void get_nextval(SString &T, int &nextval[]) 
{
	i = 1; nextval[1] = 0; j = 0;
	while (i < T[0]) {
		if (j == 0 || T[i] == T[j])
		{
			++i; ++j;
			if (T[i] != T[j]) next[i] = j;
			else nextval[i] = nextval[j];
		}
		else j = nextval[j];
	}
} // get_nextval